题目内容
已知数列{an}的前n项和Sn满足Sn+1=kSn+2(n∈N*),且a1=2,a2=1
(I)求k的值和Sn的表达式;
(II)是否存在正整数m,n,使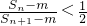 成立?若存在,则求出这样的正整数;若不存在,请说明理由.
成立?若存在,则求出这样的正整数;若不存在,请说明理由.
解:(I)∵S2=kS1+2,∴a1+a2=ka1+2又a1=2,a2=1,2+1=2k+2,∴ …(2分)
…(2分)
∴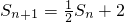 ①当n≥2时,
①当n≥2时,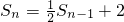 ②①-②,得
②①-②,得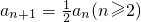
又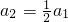 ,由a1=2≠0可得an≠0(n∈N*),∴
,由a1=2≠0可得an≠0(n∈N*),∴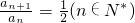
于是{an}是等比数列,其首项为a1=2,公比为 ,所以
,所以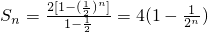 …(6分)
…(6分)
(II)不等式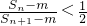 ,即
,即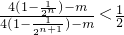 .,整理得
.,整理得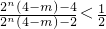 ,
,
令t=2n(4-m),则不等式变为 ,解之得2<t<6即2<2n(4-m)<6…(8分)
,解之得2<t<6即2<2n(4-m)<6…(8分)
假设存在正整数m,n使得上面的不等式成立,由于2n为偶数,4-m为整数,
则只能是2n(4-m)=4∴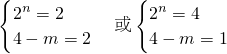
因此,存在正整数 .…(12分)
.…(12分)
分析:(I)由题设条件Sn+1=kSn+2(n∈N*),且a1=2,a2=1,利用S2=kS1+2,建立方程求出k,再利用an=Sn-Sn-1,研究数列的性质,根据数列的性质得出Sn的表达式;
(II)假设存在正整数m,n,使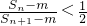 成立,由不等式进行等价转化,得出正整数m,n满足的条件,若能解出正整数m,n的值,则说明假设成立,否则说明不存在正整数m,n,使
成立,由不等式进行等价转化,得出正整数m,n满足的条件,若能解出正整数m,n的值,则说明假设成立,否则说明不存在正整数m,n,使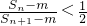 成立.
成立.
点评:本题考查数列与不等式的综合,解题的关键是充分利用题设中的恒等式进行变换,解得数列的性质,求出数列的和的表达式,本题第二小问是一个存在性问题的探究,此类题一般是假设所研究的结论成立,由此寻求其等价条件,得出参数所满足的不等式或者方程,由此方程或者不等式求解参数的可能值,若能求出符合条件的值,则说明存在这样的参数使得结论成立
 …(2分)
…(2分)∴
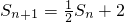 ①当n≥2时,
①当n≥2时,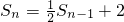 ②①-②,得
②①-②,得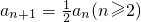
又
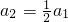 ,由a1=2≠0可得an≠0(n∈N*),∴
,由a1=2≠0可得an≠0(n∈N*),∴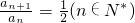
于是{an}是等比数列,其首项为a1=2,公比为
 ,所以
,所以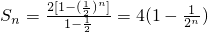 …(6分)
…(6分)(II)不等式
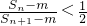 ,即
,即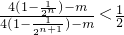 .,整理得
.,整理得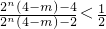 ,
,令t=2n(4-m),则不等式变为
 ,解之得2<t<6即2<2n(4-m)<6…(8分)
,解之得2<t<6即2<2n(4-m)<6…(8分)假设存在正整数m,n使得上面的不等式成立,由于2n为偶数,4-m为整数,
则只能是2n(4-m)=4∴
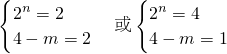
因此,存在正整数
 .…(12分)
.…(12分)分析:(I)由题设条件Sn+1=kSn+2(n∈N*),且a1=2,a2=1,利用S2=kS1+2,建立方程求出k,再利用an=Sn-Sn-1,研究数列的性质,根据数列的性质得出Sn的表达式;
(II)假设存在正整数m,n,使
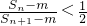 成立,由不等式进行等价转化,得出正整数m,n满足的条件,若能解出正整数m,n的值,则说明假设成立,否则说明不存在正整数m,n,使
成立,由不等式进行等价转化,得出正整数m,n满足的条件,若能解出正整数m,n的值,则说明假设成立,否则说明不存在正整数m,n,使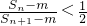 成立.
成立.点评:本题考查数列与不等式的综合,解题的关键是充分利用题设中的恒等式进行变换,解得数列的性质,求出数列的和的表达式,本题第二小问是一个存在性问题的探究,此类题一般是假设所研究的结论成立,由此寻求其等价条件,得出参数所满足的不等式或者方程,由此方程或者不等式求解参数的可能值,若能求出符合条件的值,则说明存在这样的参数使得结论成立

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知数列{an}的前n项和Sn=an2+bn(a、b∈R),且S25=100,则a12+a14等于( )
| A、16 | B、8 | C、4 | D、不确定 |