Question

17．边长为1的正方形ABCD中，边AB，BC上分别有一动点Q，R．且|BQ|=|CR|，建立适当的坐标系，求直线AR与DQ的交点P的轨迹方程．

Answer 1

分析 首先分别以AB、AD所在直线为x轴、y轴建立平面直角坐标系，设出动点P、Q、R的坐标，由平面几何知识列等式，消去参数变量即可求得点P的轨迹方程．

解答 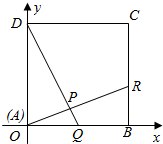解：分别以AB、AD所在直线为x轴、y轴建立平面直角坐标系，
如图所示，
则点A（0，0），B（1，0），C（1，1），D（0，1），
设动点P（x，y），设|AQ|=t（0≤t≤1），则Q（t，0），
由|BQ|=|CR|，知|AQ|=|BR|，
∴R（1，t），
当t≠0时，直线AR的方程为y=tx①，
直线DQ方程为$\frac{x}{t}+y=1$②，
由②式得，1-y=$\frac{x}{t}$③，
①×③得，y（1-y）=tx•$\frac{x}{t}$，化简得：x²+y²-y=0．
当t=0时，点P与原点重合，坐标O（0，0）满足上述方程，
故点P的轨迹方程为x²+y²-y=0（0$≤x≤\frac{1}{2}$，0$≤y≤\frac{1}{2}$）．

点评 本题考查轨迹方程的求法，正确建系并适当引用参数是解答该题的关键，是中档题．