题目内容
已知椭圆
+
=1左焦点是F1，右焦点是F2，右准线是l，P是l上一点，F1P与椭圆交于点Q，满足2
+3
=
，则|QF2|等于（ ）
| x2 |
| 5 |
| y2 |
| 4 |
| F1P |
| PQ |
| 0 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：先求出焦点坐标及准线方程，由向量间的关系得出 点Q 分有向线段F1P 成的比为λ=
，由定比分点坐标公式求得 Q的横坐标，
代入椭圆的方程可得Q的纵坐标，进而求得|QF2|．
| 1 |
| 2 |
代入椭圆的方程可得Q的纵坐标，进而求得|QF2|．
解答：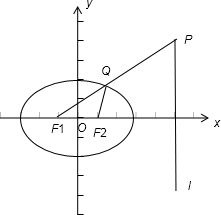
解：如图F1（-1，0）、F2（1，0），右准线l方程x=5，
∵2
+3
=
，∴
+
=
，
∴
=
，QP=2QF1，∴点 Q 分有向线段F1P 成的比为λ=
，
设 Q（m，n），则由定比分点坐标公式得m=
=1，
把Q（m，n）代入椭圆的方程得 n=±
，
∴|QF2|=
，
故选B．
解：如图F1（-1，0）、F2（1，0），右准线l方程x=5，∵2
| F1P |
| PQ |
| 0 |
| F1Q |
| QP |
| 3 |
| 2 |
| QP |
∴
| F1Q |
| 1 |
| 2 |
| QP |
| 1 |
| 2 |
设 Q（m，n），则由定比分点坐标公式得m=
-1+
| ||
1+
|
把Q（m，n）代入椭圆的方程得 n=±
4
| ||
| 5 |
∴|QF2|=
4
| ||
| 5 |
故选B．
点评：本题考查椭圆的简单性质、向量运算，以及定比分点坐标公式的应用，体现了数形结合的数学思想．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知有相同两焦点F1、F2的椭圆
+y2=1和双曲线
-y2=1，P是它们的一个交点，则△F1PF2的形状是（ ）
| x2 |
| 5 |
| x2 |
| 3 |
| A、锐角三角形 |
| B、B直角三角形 |
| C、钝有三角形 |
| D、等腰三角形 |