题目内容
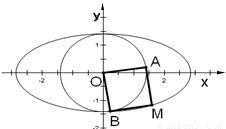
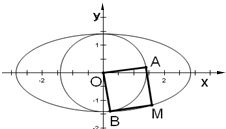 如图,过椭圆C:
如图,过椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| π |
| 2 |
分析:由∠AMB=90°及圆的性质,可得 |OM|=
b,故|OM|2=2b2≤a2,a2≤2c2,由此可得到椭圆离心率的取值范围.
| 2 |
解答:解:由∠APB=90°及圆的性质,
可得 |OM|=
b,∴|OM|2=2b2≤a2,
∴a2≤2c2∴e2≥
,
≤e<1.
故答案为:[
,1)
可得 |OM|=
| 2 |
∴a2≤2c2∴e2≥
| 1 |
| 2 |
| ||
| 2 |
故答案为:[
| ||
| 2 |
点评:本题考查直线和椭圆的位置关系和应用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件.

练习册系列答案
相关题目
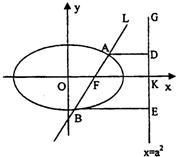 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: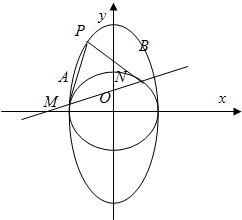 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: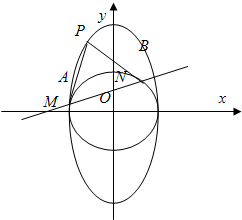 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: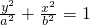 (a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.
(a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.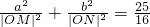 ,求椭圆C的方程;
,求椭圆C的方程; +
+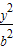 =1(a>b>0)上的动点M引圆O:x2+y2=b2的两条切线MA,MB,其中A,B分别为切点,,若椭圆上存在点M,使∠BMA=
=1(a>b>0)上的动点M引圆O:x2+y2=b2的两条切线MA,MB,其中A,B分别为切点,,若椭圆上存在点M,使∠BMA=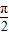 ,则该椭圆的离心率为 .
,则该椭圆的离心率为 .