题目内容
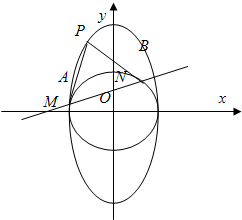 附加题:如图,过椭圆C:
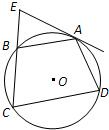
附加题:如图,过椭圆C: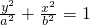 (a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.
(a>b>0)上一动点P引圆x2+y2=b2的两条切线PA,PB(A,B为切点).直线AB与x轴、y轴分别交于M、N两点.
①已知P点的坐标为(x0,y0),并且x0•y0≠0,试求直线AB的方程;
②若椭圆的短轴长为8,并且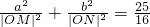 ,求椭圆C的方程;
,求椭圆C的方程;
③椭圆C上是否存在P,由P向圆O所引两条切线互相垂直?若存在,求出存在的条件;若不存在,说明理由.
解:(1)设A (x1,y1),B (x2,y2)切线PA:x1x+y1y=b2,PB:x2x+y2y=b2,
∵P点在切线PA、PB上,∴x1x0+y1y0=b2,x2x0+y2y0=b2.
∴直线AB的方程为x0x+y0y=b2.
(2)在x0x+y0y=b2中,2b=8?b=4,b2=16,
分别令y=0,得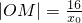 ,x=0 得
,x=0 得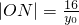
代入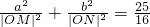 ,得:
,得: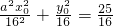 ①
①
又P(x0,y0)在椭圆上: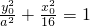 ②
②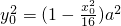 代入①?a2=25∴所求椭圆为:
代入①?a2=25∴所求椭圆为: (xy≠0)
(xy≠0)
(3)假设存在点P(x0,y0)满足PA⊥PB,连OA、OB,
由|PA|=|PB|,知四边形PAOB为正方形,|OP|= |OA|∴x02+y02=2b2①又P在椭圆上∴a2x02+b2y02=a2b2②
|OA|∴x02+y02=2b2①又P在椭圆上∴a2x02+b2y02=a2b2②
由①、②知: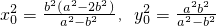 ∵a>b>0∴a2>b2,
∵a>b>0∴a2>b2,
所以 当a2≥2b2>0,即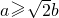 时,椭圆C上存在点P1满足条件,
时,椭圆C上存在点P1满足条件,
当a2<2b2,即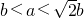 时,椭圆C上不存在满足条件的点P.
时,椭圆C上不存在满足条件的点P.
分析:(1)设A (x1,y1),B (x2,y2),切线PA:x1x+y1y=b2,PB:x2x+y2y=b2,由P点在切线PA、PB上,能求出直线AB的方程.
(2)在x0x+y0y=b2中,2b=8?b=4,b2=16,分别令y=0,得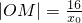 ,x=0 得
,x=0 得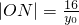 .代入
.代入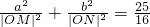 ,得:
,得: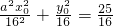 .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.
(3)假设存在点P(x0,y0)满足PA⊥PB,连OA、OB,由|PA|=|PB|,知四边形PAOB为正方形,|OP|= |OA|.所以x02+y02=2b2,又P在椭圆上,所以a2x02+b2y02=a2b2,所以
|OA|.所以x02+y02=2b2,又P在椭圆上,所以a2x02+b2y02=a2b2,所以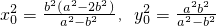 .由此知当a2≥2b2>0时,椭圆C上存在点P1满足条件,当a2<2b2时,椭圆C上不存在满足条件的点P.
.由此知当a2≥2b2>0时,椭圆C上存在点P1满足条件,当a2<2b2时,椭圆C上不存在满足条件的点P.
点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.
∵P点在切线PA、PB上,∴x1x0+y1y0=b2,x2x0+y2y0=b2.
∴直线AB的方程为x0x+y0y=b2.
(2)在x0x+y0y=b2中,2b=8?b=4,b2=16,
分别令y=0,得
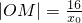 ,x=0 得
,x=0 得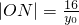
代入
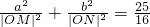 ,得:
,得: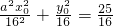 ①
①又P(x0,y0)在椭圆上:
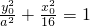 ②
②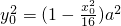 代入①?a2=25∴所求椭圆为:
代入①?a2=25∴所求椭圆为: (xy≠0)
(xy≠0)(3)假设存在点P(x0,y0)满足PA⊥PB,连OA、OB,
由|PA|=|PB|,知四边形PAOB为正方形,|OP|=
 |OA|∴x02+y02=2b2①又P在椭圆上∴a2x02+b2y02=a2b2②
|OA|∴x02+y02=2b2①又P在椭圆上∴a2x02+b2y02=a2b2②由①、②知:
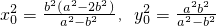 ∵a>b>0∴a2>b2,
∵a>b>0∴a2>b2,所以 当a2≥2b2>0,即
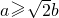 时,椭圆C上存在点P1满足条件,
时,椭圆C上存在点P1满足条件,当a2<2b2,即
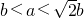 时,椭圆C上不存在满足条件的点P.
时,椭圆C上不存在满足条件的点P.分析:(1)设A (x1,y1),B (x2,y2),切线PA:x1x+y1y=b2,PB:x2x+y2y=b2,由P点在切线PA、PB上,能求出直线AB的方程.
(2)在x0x+y0y=b2中,2b=8?b=4,b2=16,分别令y=0,得
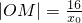 ,x=0 得
,x=0 得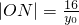 .代入
.代入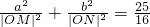 ,得:
,得: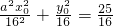 .由此能求出椭圆C的方程.
.由此能求出椭圆C的方程.(3)假设存在点P(x0,y0)满足PA⊥PB,连OA、OB,由|PA|=|PB|,知四边形PAOB为正方形,|OP|=
 |OA|.所以x02+y02=2b2,又P在椭圆上,所以a2x02+b2y02=a2b2,所以
|OA|.所以x02+y02=2b2,又P在椭圆上,所以a2x02+b2y02=a2b2,所以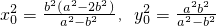 .由此知当a2≥2b2>0时,椭圆C上存在点P1满足条件,当a2<2b2时,椭圆C上不存在满足条件的点P.
.由此知当a2≥2b2>0时,椭圆C上存在点P1满足条件,当a2<2b2时,椭圆C上不存在满足条件的点P.点评:本题主要考查直线与圆锥曲线的综合应用能力,具体涉及到轨迹方程的求法及直线与椭圆的相关知识,解题时要注意合理地进行等价转化.

练习册系列答案
相关题目
 附加题:
附加题: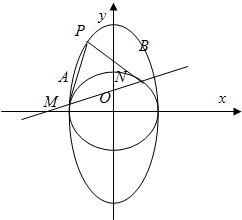 附加题:如图,过椭圆C:
附加题:如图,过椭圆C: =M
=M ,试求二阶矩阵M.
,试求二阶矩阵M. ,点F1,F2为其左、右焦点,直线l的参数方程为
,点F1,F2为其左、右焦点,直线l的参数方程为 (t为参数,t∈R).求点F1,F2到直线l的距离之和.
(t为参数,t∈R).求点F1,F2到直线l的距离之和. .
.