题目内容
12. 已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.
已知平行六面体ABCD-A1B1C1D1,AC1与平面A1BD,CB1D1交于E,F两点.以下命题中真命题有①②④_(写出所有正确命题的序号)
①点E,F为线段AC1的两个三等分点;
②四面体AB1CD1的体积是平行六面体ABCD-A1B1C1D1体积的三分之一;
③E为△A1BD的内心;
④若∠A1AB=∠A1AD=∠BAD,AA1=AB=AD,则AC1⊥面A1BD.
分析 ①在对角面ACC1A1中可看出点E,F为线段AC1的两个三等分点,正确;
②四面体AB1CD1可以看作是一个平行六面体裁去四个角,很容易证明是正确的;
③A1E为△A1BD的边BD的中线,故E不一定为△A1BD的内心(实际上是重心),故错误;
④根据线面垂直,推出线线垂直,再推出线面垂直,正确.
解答 解:①如图,在对角面ACC1A1中可看出点E,F为线段AC1的两个三等分点,正确;
②四面体AB1CD1可以看作是一个平行六面体裁去四个角,
设平行六面体的边长a,每个角体积为$\frac{{a}^{3}}{6}$,剩下a3-4×$\frac{{a}^{3}}{6}$=$\frac{1}{3}{a}^{3}$,正确;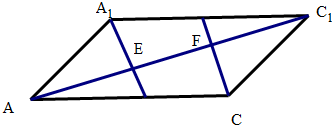
③A1E为△A1BD的边BD的中线,故E不一定为△A1BD的内心(实际上是重心),故错误;
④如图:
BD⊥AC,BD⊥A1E(两个等腰三角形),
∴BD⊥平面AA1C1C,
∵AC1∈AA1C1C,
∴AC1⊥BD;
同理可证 AC1⊥A1B AC1⊥A1D,
可证AC1⊥平面A1BD.
故答案为:①②④.
点评 本题考查了平行六面体的结构特征、重心、线面垂直的证明方法,属于中档题.

练习册系列答案
 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案
相关题目
3.函数f(x)=x3+3ax2+3[(a+2)x+1]有极大值又有极小值,则a的取值范围是( )
| A. | (-1,2) | B. | f(-2,1) | C. | (-∞,-1)∪(2,+∞) | D. | (-∞,-2)∪(1,+∞) |
17.已知罗坊会议纪念馆对每日参观人数量拥挤等级规定如表:
该纪念馆对3月份的参观人数量作出如图的统计数据:

(1)某人3月份连续2天到该纪念馆参观,求这2天他遇到的拥挤等级均为良的概率;
(2)从该纪念馆3月份参观人数低于100人的天数中随机选取3天,记这3天拥挤等级为优的天数为ξ,求ξ的分布列及数学期望.
| 参观人数量 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | >300 |
| 拥挤等级 | 优 | 良 | 轻度拥挤 | 中度拥挤 | 重度拥挤 | 严重拥挤 |

(1)某人3月份连续2天到该纪念馆参观,求这2天他遇到的拥挤等级均为良的概率;
(2)从该纪念馆3月份参观人数低于100人的天数中随机选取3天,记这3天拥挤等级为优的天数为ξ,求ξ的分布列及数学期望.
