题目内容
甲、乙两位学生参加数学竞赛培训。现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲 82 81 79 78 95 88 93 84
乙 92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据,并指出两组数据的中位数。
(2)从平均数、方差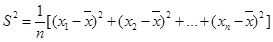 考虑,你认为哪位学生更稳定?请说明理由。
考虑,你认为哪位学生更稳定?请说明理由。
(Ⅰ) 作出茎叶图如下: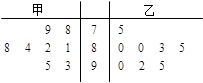
(Ⅱ)甲的成绩较稳定,派甲参赛比较合适.
解析试题分析:(1)根据所给的数据,以十位做茎,个位做叶,做出茎叶图,注意图形要做到美观,不要丢失数据.
(2)根据所给的数据做出两个人的平均数和方差,把平均数和方差进行比较,得到两个人的平均数相等,但是乙的方差大于甲的方差,得到要派甲参加.
解:(Ⅰ) 作出茎叶图如下: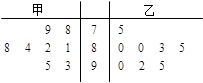
(Ⅱ)派甲参赛比较合适.理由如下: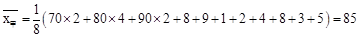 ,
, ,
,
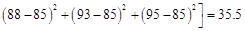 ,
,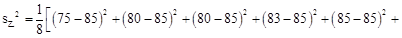
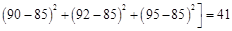
∵
 ,
,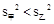 ,∴甲的成绩较稳定,派甲参赛比较合适.
,∴甲的成绩较稳定,派甲参赛比较合适.
考点:本试题主要考查了对于两组数据,通常要求的是这组数据的方差和平均数,用这两个特征数来表示分别表示两组数据的特征,即平均水平和稳定程度.
点评:解决该试题的关键是理解方差和平均数各自代表的含义。

 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案(本题满分12分)
对某校高二年级学生参加社会实践活动次数进行统计,随机抽取M名学生作为样本,得到这M名学生参加社会实践活动的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
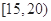 | 26 | n |
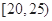 | m | P |
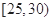 | 1 | 0.025 |
| 合计 | M | 1 |
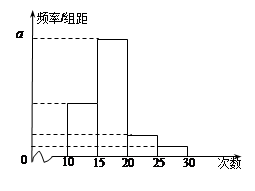
(Ⅰ)求出表中M,P及图中
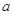 的值;
的值;(Ⅱ)在所取样本中,从参加社会实践活动的次数不少于20次的学生中任选2人,求恰有一人参加社会实践活动次数在区间
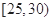 内的概率.
内的概率. (本题满分10分)对某校高三年级学生参加社区服务次数进行统计,随机抽取 名学生作为样本,得到这
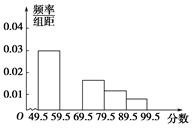
名学生作为样本,得到这 名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
名学生参加社区服务的次数.根据此数据作出了频数与频率的统计表和频率分布直方图如下:
| 分组 | 频数 | 频率 |
 | 10 | 0.25 |
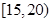 | 24 |  |
 |  |  |
 | 2 | 0.05 |
| 合计 |  | 1 |

(Ⅰ)求出表中
 及图中
及图中 的值;
的值;(Ⅱ)若该校高三学生有240人,试估计该校高三学生参加社区服务的次数在区间
 内的人数;
内的人数;(Ⅲ)在所取样本中,从参加社区服务的次数不少于20次的学生中任选2人,求至多一人参加社区服务次数在区间
 内的概率.
内的概率. (本小题满分12分)
以下是测得的某种产品的广告费支出x与销售额y(单位:百万元)之间,有如下的对应数据:
| 广告费支出x | 2 | 4 | 5 | 6 | 8 |
| 销售额y | 30 | 40 | 60 | 50 | 70 |
(2)求y关于x的回归直线方程;
(3)预测当广告费支出为2(百万元)时,则这种产品的销售额为多少(百万元)
某种产品的广告费支出x与销售额y(单位:百万元)之间的一般规律:
某车间为了规定工时定额,需要确定加个某零件所花费的时间,为此作了四次实验,得到的数据如下:
| 零件的个数x(个) | 2 | 3 | 4 | 5 |
| 加工的时间y(小时) | 2.5 | 3 | 4 | 4.5 |
(2) 试预测加工10个零件需要多少时间?

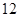 名男志愿者和
名男志愿者和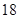 名女志愿者,调查发现,这
名女志愿者,调查发现,这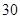 名志愿者的身高如下:(单位:cm )
名志愿者的身高如下:(单位:cm )
 cm以上(包括
cm以上(包括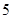 人,再从这
人,再从这 人,则至少有一人是“高个子”的概率是多少?
人,则至少有一人是“高个子”的概率是多少?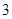 名志愿者,用
名志愿者,用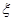 表示所选志愿者中能担任“礼仪小姐”的人数,试写出
表示所选志愿者中能担任“礼仪小姐”的人数,试写出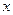 (吨)与相应的生产能耗
(吨)与相应的生产能耗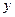 (吨标准煤)的几组对照数据
(吨标准煤)的几组对照数据
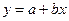 ;
;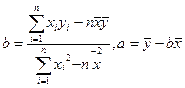 )
)