题目内容
动点P(a,b)在不等式组
|
| a+b-3 |
| a-1 |
分析:本题是不等式中线性规划的延伸题,不再求线性目标函数的最值,转而求w=
的取值范围,可看成是某两点的斜率问题
| a+b-3 |
| a-1 |
解答: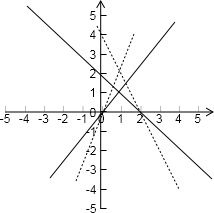 解:w=
解:w=
=
=1+
,
作出可行域,分析可得:
点(a,b)与点(1,2)确定的直线的斜率为(-∞,-2]∪[2,+∞),
从而可以求得w的取值范围为(-∞,-1]∪[3,+∞);
故答案为(-∞,-1]∪[3,+∞).
 解:w=
解:w=| a+b-3 |
| a-1 |
| a-1+b-2 |
| a-1 |
| b-2 |
| a-1 |
作出可行域,分析可得:
点(a,b)与点(1,2)确定的直线的斜率为(-∞,-2]∪[2,+∞),
从而可以求得w的取值范围为(-∞,-1]∪[3,+∞);
故答案为(-∞,-1]∪[3,+∞).
点评:本题主要考查了线性规划中最值问题,转化为直线的斜率,利用了其几何意义进行求解

练习册系列答案
相关题目
 已知:点P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线,如图所示.
已知:点P为线段AB上的动点(与A,B两点不重合).在同一平面内,把线段AP,BP分别折成△CDP,△EFP,其中∠CDP=∠EFP=90°,且D,P,F三点共线,如图所示. 。
。 。
。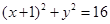 上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且
上的一动点,点D(1,0),点M是DN的中点,点P在线段CN上,且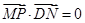 .
.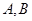 ,当动点P与A,B不重合时,设直线
,当动点P与A,B不重合时,设直线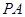 与
与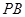 的斜率分别为
的斜率分别为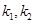 ,证明:
,证明: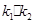 为定值;
为定值;