题目内容
等差数列{an}、{bn}的前n项和分别为Sn、Tn,且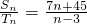 ,则使得
,则使得 为整数的正整数的n的个数是
为整数的正整数的n的个数是
- A.3
- B.4
- C.5
- D.6
C
分析:由等差数列{an}、{bn},利用等差数列的性质表示出an和bn,将 分子分母同时乘以n,将表示出的an与bn代入,再利用等差数列的前n项和公式变形,根据已知的等式化简,整理后将正整数n代入进行检验,即可得到
分子分母同时乘以n,将表示出的an与bn代入,再利用等差数列的前n项和公式变形,根据已知的等式化简,整理后将正整数n代入进行检验,即可得到 为整数的正整数的n的个数.
为整数的正整数的n的个数.
解答:∵等差数列{an}、{bn},
∴an=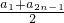 ,bn=
,bn=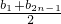 ,
,
∴ =
=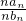 =
= =
=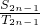 ,又
,又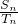 =
=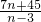 ,
,
∴ =
=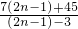 =7+
=7+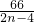 ,
,
经验证,当n=1,3,5,13,35时, 为整数,
为整数,
则使得 为整数的正整数的n的个数是5.
为整数的正整数的n的个数是5.
故选C
点评:此题考查了等差数列的性质,以及等差数列的前n项和公式,熟练掌握性质及公式是解本题的关键.
分析:由等差数列{an}、{bn},利用等差数列的性质表示出an和bn,将
 分子分母同时乘以n,将表示出的an与bn代入,再利用等差数列的前n项和公式变形,根据已知的等式化简,整理后将正整数n代入进行检验,即可得到
分子分母同时乘以n,将表示出的an与bn代入,再利用等差数列的前n项和公式变形,根据已知的等式化简,整理后将正整数n代入进行检验,即可得到 为整数的正整数的n的个数.
为整数的正整数的n的个数.解答:∵等差数列{an}、{bn},
∴an=
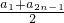 ,bn=
,bn=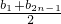 ,
,∴
 =
=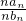 =
= =
=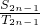 ,又
,又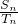 =
=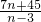 ,
,∴
 =
=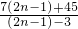 =7+
=7+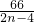 ,
,经验证,当n=1,3,5,13,35时,
 为整数,
为整数,则使得
 为整数的正整数的n的个数是5.
为整数的正整数的n的个数是5.故选C
点评:此题考查了等差数列的性质,以及等差数列的前n项和公式,熟练掌握性质及公式是解本题的关键.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目