题目内容

若(a+b+c)(b+c－a)=3bc,且sinA=2sinBcosC, 那么ΔABC是    （    ）

A．直角三角形                           B．等腰直角三角形   

C．等腰三角形                           D．等边三角形

 

【答案】

D

【解析】因为(a+b+c)(b+c－a)=3bc,且sinA=2sinBcosC,

解：∵（a+b+c）（b+c-a）=3bc∴[（b+c）+a][（b+c）-a]=3bc∴（b+c）2-a2=3bc

b2+2bc+c2-a2=3bc,b2-bc+c2=a2

根据余弦定理有a2=b2+c2-2bccosA

∴b2-bc+c2=a2=b2+c2-2bccosA

bc=2bccosAcosA=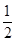∴A=60°又由sinA=2sinBcosC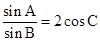，,解得b=c,故三角形为．等边三角形，选D

 

练习册系列答案
相关题目
5、已知a，b，c∈R，命题“若a+b+c=3，则a2+b2+c2≥3”的否命题是（　　）
下列命题中正确的有
②③④
②③④
（填序号）
①若
a
与
b
满足
a
•
b
＞0，则
a
与
b
所成的角为锐角；
②若
a
与
b
不共线，
m
=λ1
a
+λ2
b
，
n
=μ1
a
+μ2
b
（λ1，λ2，μ1，μ2∈R），则
m
∥
n
的充要条件是λ1μ2-λ2μ1=0；
③若
OA
+
OB
+
OC
=
O
，且|
OA
|=|
OB
|=|
OC
|，则△ABC是等边三角形；
④若
a
与
b
为非零向量，且
a
⊥
b
，则|
a
+
b
|=|
a
-
b
|；
⑤设
a
，
b
，
c
为非零向量，若
a
•
b
=
c
•
b
，则
a
=
c
；
⑥若
a
，
b
，
c
为非零向量，则
a
•(
b
•
c
)=(
a
•
b
)•
c
．

若a＞c，且b＋c＞0，则不等式＞0的解集是

[　　]
A．

{x|－a＜x＜b，或x＞c}

B．

{x|－a＜x＜c，或x＞b}

C．

{x|－b＜x＜a，或x＞c}

D．

{x|－b＜x＜c，或x＞a}

在以下命题中：

①|a|－|b|＝|a＋b|是a、b共线的充要条件；

②若a∥b，则存在唯一的实数λ，使a＝λb；

③对空间任意一点O和不共线的三点A、B、C，若＝2－2－，则P、A、B、C四点共面；

④若{a，b，c}为空间一个基底，则{a＋b，b＋c，c＋a}构成空间另一个基底；

⑤|(a·b)c|＝|a||b||c|．

其中不正确的个数为

[　　]
A．

2

B．

3

C．

4

D．

5

以下有四个命题：
①一个等差数列{an}中，若存在ak+1＞ak＞O（k∈N），则对于任意自然数n＞k，都有an＞0；
②一个等比数列{an}中，若存在ak＜0，ak+1＜O（k∈N），则对于任意n∈N，都有an＜0；
③一个等差数列{an}中，若存在ak＜0，ak+1＜0（k∈N），则对于任意n∈N，都有an＜O；
④一个等比数列{an}中，若存在自然数k，使ak•ak+1＜0，则对于任意n∈N，都有an．an+1＜0；
其中正确命题的个数是


  1. A.
    0个
  2. B.
    1个
  3. C.
    2个
  4. D.
    3个

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网