题目内容
已知:函数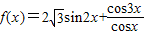 .
.(1)求函数f(x)的最大值及此时x的值;
(2)在△ABC中,a,b,c分别为内角A,B,C所对的边,且对f(x)定义域中的任意的x都有f(x)≤f(A).现在给出三个条件:①a=2;②B=45°;③
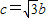 ,试从中选出两个可以确定△ABC的条件,写出你的选择并以此为依据求△ABC的面积.(只需写出一个选定方案即可)
,试从中选出两个可以确定△ABC的条件,写出你的选择并以此为依据求△ABC的面积.(只需写出一个选定方案即可)
【答案】分析:(1)由已知中函数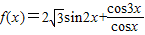 .利用两角和的余弦公式,及二倍角公式,辅助角公式,可以将式子化简为一个正弦型函数的形式,根据正弦型函数的性质,即可得到答案.
.利用两角和的余弦公式,及二倍角公式,辅助角公式,可以将式子化简为一个正弦型函数的形式,根据正弦型函数的性质,即可得到答案.
(2)由已知中对f(x)定义域中的任意的x都有f(x)≤f(A),我们易求出A的大小,结合:①a=2;②B=45°;③ ,易求出△ABC的面积.
,易求出△ABC的面积.
解答:解:(1)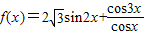
=
=
=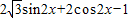
= …4分
…4分
所以当 =2kπ+
=2kπ+ ,k∈Z时,f(x)取最大值3,
,k∈Z时,f(x)取最大值3,
此时,x=kπ+ ,k∈Z;…(6分)
,k∈Z;…(6分)
(2)由f(A)是f(x)的最大值及A∈(0,π),得到,A= ,
,
方案1 选择①②…(7分)
由正弦定理 ,则b=2
,则b=2 ,
,
sinC=sin(A+B)=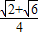 ,…(10分)
,…(10分)
所以,面积S= a•b•sinC=
a•b•sinC= +1.…(12分)
+1.…(12分)
点评:本题考查的知识点是三角函数中的恒等变换应用,三角形中的几何计算,三角函数的最值,解三角形,其中(1)的关键是化简函数的解析式为一个正弦型函数的形式,(2)的关键是求出A的大小.
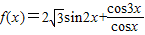 .利用两角和的余弦公式,及二倍角公式,辅助角公式,可以将式子化简为一个正弦型函数的形式,根据正弦型函数的性质,即可得到答案.
.利用两角和的余弦公式,及二倍角公式,辅助角公式,可以将式子化简为一个正弦型函数的形式,根据正弦型函数的性质,即可得到答案.(2)由已知中对f(x)定义域中的任意的x都有f(x)≤f(A),我们易求出A的大小,结合:①a=2;②B=45°;③
 ,易求出△ABC的面积.
,易求出△ABC的面积.解答:解:(1)
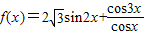
=

=

=
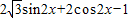
=
 …4分
…4分所以当
 =2kπ+
=2kπ+ ,k∈Z时,f(x)取最大值3,
,k∈Z时,f(x)取最大值3,此时,x=kπ+
 ,k∈Z;…(6分)
,k∈Z;…(6分)(2)由f(A)是f(x)的最大值及A∈(0,π),得到,A=
 ,
,方案1 选择①②…(7分)
由正弦定理
 ,则b=2
,则b=2 ,
,sinC=sin(A+B)=
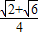 ,…(10分)
,…(10分)所以,面积S=
 a•b•sinC=
a•b•sinC= +1.…(12分)
+1.…(12分)点评:本题考查的知识点是三角函数中的恒等变换应用,三角形中的几何计算,三角函数的最值,解三角形,其中(1)的关键是化简函数的解析式为一个正弦型函数的形式,(2)的关键是求出A的大小.

练习册系列答案
 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案 高效智能课时作业系列答案
高效智能课时作业系列答案
相关题目
 ,
, ;
; 的图象;
的图象; 在区间[-1,|
在区间[-1,| |-2]上单调递增,试确定
|-2]上单调递增,试确定 .
.  的最小正周期和当
的最小正周期和当 时的值域;
时的值域;
 ,
, .求
.求 的值.
的值.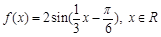 .
. 的值;
的值;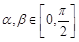 ,
,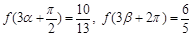 ,求
,求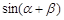 的值.
的值.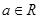 ,函数
,函数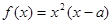 .
. 的单调递减区间;
的单调递减区间;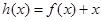 在区间
在区间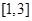 上有极值,求
上有极值,求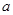 的取值范围;
的取值范围;