题目内容
设|a|= 2，|b|=1，a与b夹角为60°，要使kb – a与a垂直，则k的值为（ ）
| A．1 | B．2 | C．3 | D．4 |
D
解析试题分析：根据题意，由于|a| = 2，|b| =1，a与b夹角为60°，要使kb – a与a垂直，则满足(kb – a）a=0,即可知ab=1,那么可知k-4=0，故可知k=4,答案为D.
考点：数量积与向量垂直的关系
点评：本题考点是数量积与向量垂直的关系，直接将垂直关系转化为内积为0，通过解方程的方式求出参数的值，本题型是数量积中的常见题型，是高考的一个热点
练习册系列答案
名校课堂系列答案
相关题目
若
且
与
也互相垂直，则
的值为 （ ）
A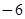． | B． | C．3 | D． |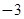
平面向量的集合
到的映射
，其中
为常向量．若映射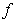
满足
对任意的
恒成立，则的坐标可能是（ ）
A．( ，) | B．(， ) | C．( ， ) | D．(，) |
已知向量
满足
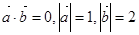，则
| A．0 | B．2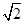 | C．4 | D．8 |
已知向量
，且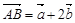
，
，
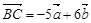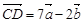，则一定共线的三点是( )
| A．A、C、D | B．A、B、D | C．A、B、C | D．B、C、D |
设为基底向量,已知向量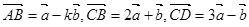
,若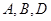
三点共线,则实数
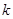的值等于
A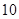． | B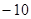． | C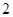． | D． |
若向量方程2x－3(x－2a)＝0，则向量x等于( )
A． a | B．－6a | C．6a | D．－a |
已知向量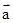
＝（3，4），
＝（2，－1），如果向量
与垂直，则实数k的值为
A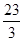． | B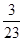． | C．2 | D．－ |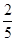
若第一象限内的点
，落在经过点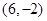
且具有方向向量
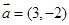的直线
上，则
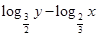有 （ ）
A．最大值 | B．最大值1 | C．最小值 | D．最小值1 |