题目内容
15．下列函数中，在区间（0，+∞）上为增函数的是（ ）| A． | f（x）=-$\sqrt{x+1}$ | B． | f（x）=${（\frac{1}{2}）}^{x}$ | C． | f（x）=lnx+2 | D． | f（x）=x+$\frac{1}{x}$ |
分析 根据基本初等函数的单调性判断即可．
解答 解：A、f（x）=-$\sqrt{x+1}$，当x≥-1时，函数f（x）为减函数，
B、f（x）=$（\frac{1}{2}）^{x}$是减函数，
C、f（x）=lnx+2，在（0，+∞）上是增函数，
D、f（x）=x+$\frac{1}{x}$在（0，1）为减函数，在（1，+∞）上是增函数，
故选C．
点评 此题主要考查函数单调性的判断，掌握基本初等函数的单调性是关键．
练习册系列答案
相关题目
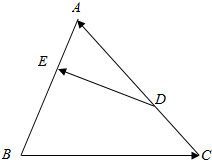如图，在△ABC中，D、E分别为AC，AB边上的点，$\frac{CD}{DA}$=$\frac{AE}{EB}$=$\frac{1}{2}$，记$\overrightarrow{BC}$=$\overrightarrow{a}$，$\overrightarrow{CA}$=$\overrightarrow{b}$．求证：$\overrightarrow{DE}$=$\frac{1}{3}$（$\overrightarrow{b}$-$\overrightarrow{a}$）．
10．设a＞0，b＞0若$\sqrt{{3}^{5}}$是3a与3b的等比中项，则$\frac{1}{a}+\frac{1}{b}$的最小值为（ ）
| A． | $\frac{8}{3}$ | B． | $\frac{4}{5}$ | C． | 4 | D． | $\frac{1}{4}$ |
7．已知f（3${\;}^{{x}^{2}-1}$）的定义域是[-1，1]，则f（log3x）的定义域是（ ）
| A． | （0，$\root{3}{3}$） | B． | [$\root{3}{3}$，3] | C． | [3，+∞） | D． | （0，3] |