题目内容
(2011•渭南三模)已知椭圆C:
+
=1(a>b>0)的左、右焦点分别为F1,F2,短轴的一个端点为B且
•
=0,直线x-y+b=0是抛物线y2=4x的一条切线.
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点S(0,-
)的动直线l交椭圆C于M、N两点.问:是否存在一个定点T,使得以MN为直径的圆恒过点T?若存在,求点T坐标;若不存在,说明理由.
| x2 |
| a2 |
| y2 |
| b2 |
| BF1 |
| BF2 |
(Ⅰ)求椭圆C的方程;
(Ⅱ)过点S(0,-
| 1 |
| 3 |
分析:(Ⅰ)由
,得x2+(2b-4)x+b2=0,因直线y=x-b与抛物线y2=4x相切,△=(2b-4)2-4b2=0,解得b=1.由短轴的一个端点为B且
•
=0,知a=
b=
.由此能求出椭圆方程.
(Ⅱ)当l与x轴平行时,以MN为直径的圆的方程:x2+(y+
)2=
.当l与x轴垂直时,以MN为直径的圆的方程:x2+y2=1.由
解得两圆公共点(0,1).因此,所求的点T如果存在,只能是(0,1).(ⅰ)当直线L斜率不存在时,以MN为直径的圆过点T(0,1);(ⅱ)若直线L斜率存在时,可设直线l:y=kx-
,由
,得(18k2+9)x2-12kx-16=0,记点M(x1,y1)、N(x2,y2),由韦达定理和向量数量积公式能推导出TM⊥TN,综合(ⅰ)(ⅱ),以MN为直径的圆恒过点T(0,1).
|
| BF1 |
| BF2 |
| 2 |
| 2 |
(Ⅱ)当l与x轴平行时,以MN为直径的圆的方程:x2+(y+
| 1 |
| 3 |
| 16 |
| 9 |
|
| 1 |
| 3 |
|
解答:解:(Ⅰ)由
,得x2+(2b-4)x+b2=0,
因直线y=x+b与抛物线y2=4x相切,
∴△=(2b-4)2-4b2=0,
∴b=1.…2分
∵短轴的一个端点为B且
•
=0,
∴a=
b=
.…4分
故所求椭圆方程为
+y2=1.…5分
(Ⅱ)当l与x轴平行时,以MN为直径的圆的方程:x2+(y+
)2=
.
当l与x轴垂直时,以MN为直径的圆的方程:x2+y2=1.
由
解得
,
即两圆公共点(0,1).
因此,所求的点T如果存在,只能是(0,1)…7分
(ⅰ)当直线L斜率不存在时,以MN为直径的圆过点T(0,1)
(ⅱ)若直线L斜率存在时,可设直线l:y=kx-
,
由
,得(18k2+9)x2-12kx-16=0,
记点M(x1,y1)、N(x2,y2),
则
.…9分
∵
=(x1,y1-1),
=(x2,y2-1),
∴
•
=x1x2+(y1-1)(y2-1)
=x1x2+(kx1-
)(kx2-
)+
=(1+k2)x1x2-
k(x1+x2)+
=(1+k2)•
-
k•
+
=0.
∴TM⊥TN,…11分
综合(ⅰ)(ⅱ),以MN为直径的圆恒过点T(0,1).…12分
|
因直线y=x+b与抛物线y2=4x相切,
∴△=(2b-4)2-4b2=0,
∴b=1.…2分
∵短轴的一个端点为B且
| BF1 |
| BF2 |
∴a=
| 2 |
| 2 |
故所求椭圆方程为
| x2 |
| 2 |
(Ⅱ)当l与x轴平行时,以MN为直径的圆的方程:x2+(y+
| 1 |
| 3 |
| 16 |
| 9 |
当l与x轴垂直时,以MN为直径的圆的方程:x2+y2=1.
由
|
|
即两圆公共点(0,1).
因此,所求的点T如果存在,只能是(0,1)…7分
(ⅰ)当直线L斜率不存在时,以MN为直径的圆过点T(0,1)
(ⅱ)若直线L斜率存在时,可设直线l:y=kx-
| 1 |
| 3 |
由
|
记点M(x1,y1)、N(x2,y2),
则
|
∵
| TM |
| TN |
∴
| TM |
| TN |
=x1x2+(kx1-
| 4 |
| 3 |
| 4 |
| 3 |
| 16 |
| 9 |
=(1+k2)x1x2-
| 4 |
| 3 |
| 16 |
| 9 |
=(1+k2)•
| -16 |
| 18k2+9 |
| 4 |
| 3 |
| 12k |
| 18k2+9 |
| 16 |
| 9 |
=0.
∴TM⊥TN,…11分
综合(ⅰ)(ⅱ),以MN为直径的圆恒过点T(0,1).…12分
点评:本题主要考查椭圆标准方程,简单几何性质,直线与椭圆的位置关系,圆的简单性质等基础知识.考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.本题对数学思维的要求比较高,要求学生理解“存在”、“恒成立”,以及运用一般与特殊的关系进行否定,本题有一定的探索性.综合性强,难度大,易出错.

练习册系列答案
相关题目
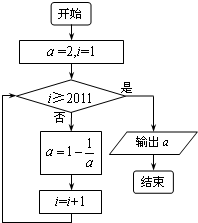 (2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( )
(2011•渭南三模)已知某程序框图如图所示,则执行该程序后输出的结果是( ) (2011•渭南三模)已知正三棱柱的侧面积为36,其三视图如图所示,则它的左视图的面积为( )
(2011•渭南三模)已知正三棱柱的侧面积为36,其三视图如图所示,则它的左视图的面积为( )