Question

(本小题满分12分)已知函数.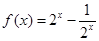

 

(1)若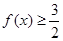，求x的取值范围；

 

(2)若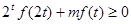对于∈[1,2]恒成立，求实数m的取值范围．

 

Answer 1

【答案】

解：(1)当x<0时，f(x)＝0；

当x≥0时，f(x)＝2^x－.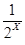

 

由条件可知2^x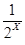－》2，即2^2x－1.5·2^x－1》0，

 

解得2^x》2

∵2^x>0，∴x》1．

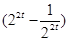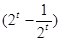(2)当t∈[1,2]时，2^t＋m≥0，

 

即m(2^2t－1)≥－(2^4t－1)．

∵2^2t－1>0，∴m≥－(2^2t＋1)．

∵t∈[1,2]，∴－(1＋2^2t)∈[－17，－5]，

故m的取值范围是[－5，＋∞)．

【解析】略