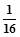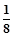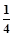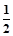题目内容
(本小题满分14分)
在等比数列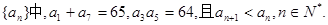
(1)求数列{an}的通项公式;
(2)求数列{an}的前5项的和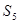 ;
;
(3)若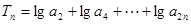 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值.
在等比数列
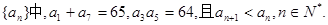
(1)求数列{an}的通项公式;
(2)求数列{an}的前5项的和
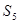 ;
;(3)若
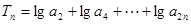 ,求Tn的最大值及此时n的值.
,求Tn的最大值及此时n的值. (1)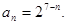 (2)
(2) 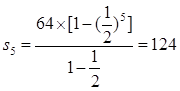
(3)当n = 3时,Tn的最大值为9lg2.
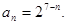 (2)
(2) 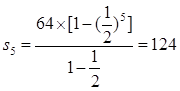
(3)当n = 3时,Tn的最大值为9lg2.
(1)由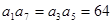 ,再结合
,再结合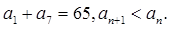 可求出
可求出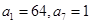 ,从而求出公比q,得到{an}的通项公式.
,从而求出公比q,得到{an}的通项公式.
(2)根据等比数列的前n项和公式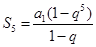 直接求S5即可.
直接求S5即可.
(3)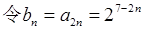 ,所以
,所以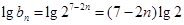 ,
,
显然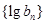 是等差数列,所以按照等差数列的前n项和公式求出
是等差数列,所以按照等差数列的前n项和公式求出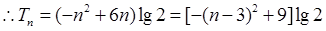 ,
,
显然当n=3时,Tn取得最大值,最大值为T3.
(1)设数列{an}的公比为q. 由等比数列性质可知:
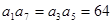 , 而
, 而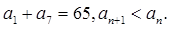
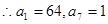 ,
,
由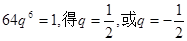 (舍),
(舍),
故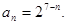
(2)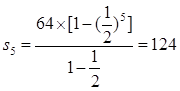
(3)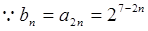
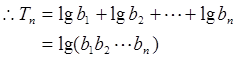
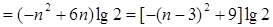
∴当n = 3时,Tn的最大值为9lg2.
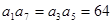 ,再结合
,再结合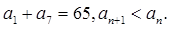 可求出
可求出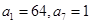 ,从而求出公比q,得到{an}的通项公式.
,从而求出公比q,得到{an}的通项公式.(2)根据等比数列的前n项和公式
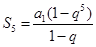 直接求S5即可.
直接求S5即可.(3)
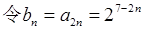 ,所以
,所以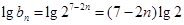 ,
,显然
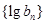 是等差数列,所以按照等差数列的前n项和公式求出
是等差数列,所以按照等差数列的前n项和公式求出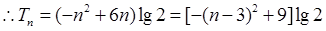 ,
,显然当n=3时,Tn取得最大值,最大值为T3.
(1)设数列{an}的公比为q. 由等比数列性质可知:
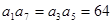 , 而
, 而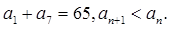
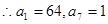 ,
, 由
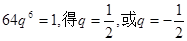 (舍),
(舍), 故
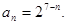
(2)
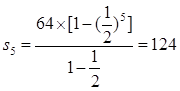
(3)
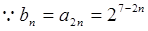
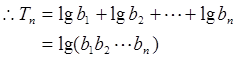
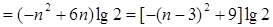
∴当n = 3时,Tn的最大值为9lg2.

练习册系列答案
相关题目
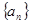 中,
中,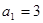 ,其前
,其前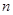 项和为
项和为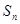 ,等比数列
,等比数列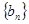 的各项均为正数,
的各项均为正数,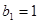 ,公比为
,公比为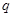 ,且
,且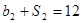 ,
, 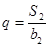 .
.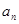 与
与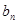 ;(Ⅱ)证明:
;(Ⅱ)证明: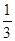 ≤
≤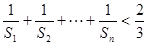 .
. 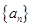 是公比为
是公比为 的等比数列,若
的等比数列,若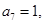 且
且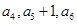 成等差数列,则实数
成等差数列,则实数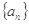 的前
的前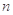 项和
项和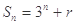 ,则
,则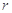 = ( )
= ( )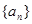 中,
中,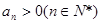 ,公比
,公比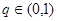 ,且
,且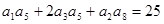 ,
,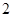 是
是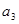 与
与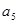 的等比中项。设
的等比中项。设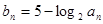 .
.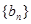 的通项公式;
的通项公式;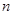 项和为
项和为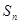 ,
,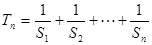 ,求
,求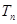 .
. 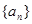 中,a1=3,前三项和为21,则a3 + a4 + a5 等于
中,a1=3,前三项和为21,则a3 + a4 + a5 等于 中
中 >0,且
>0,且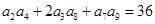 ,则
,则 =
= 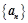 中,
中,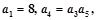 则
则 =( )
=( )