题目内容
当 时,不等式
时,不等式 恒成立,则
恒成立,则 的取值范围是 .
的取值范围是 .
【答案】
m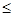 -5.
-5.
【解析】
试题分析:根据题意,由于不等式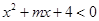 恒成立,即可知
恒成立,即可知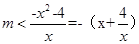 ,则只要求解函数
,则只要求解函数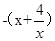 的最小值即可,结合对钩函数的性质可知,当
的最小值即可,结合对钩函数的性质可知,当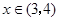 时,最小值取不到趋近于x=4的值,即可知m
时,最小值取不到趋近于x=4的值,即可知m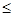 -5.。
-5.。
考点:一元二次不等式的恒成立
点评:解决的关键是根据分离参数的思想来求解参数m的范围,属于基础题。

练习册系列答案
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案
相关题目
 对一切实数
对一切实数 都有
都有
 成立,且
成立,且 .(1)求
.(1)求 的值 (2)求
的值 (2)求 ,设P:当
,设P:当 时,不等式
时,不等式 恒成立;Q:当
恒成立;Q:当 时,
时, 是单调函数。如果满足P成立的
是单调函数。如果满足P成立的 的集合记为
的集合记为 ,满足Q成立的
,满足Q成立的
 ,求
,求 (
( 为全集)
为全集) 时,不等式
时,不等式 恒成立,则实数
恒成立,则实数 取值范围是( )
取值范围是( ) ,其中
,其中 .
. ,求
,求 在
在 上的最小值;
上的最小值; 在定义域内既有极大值又有极小值,求实数
在定义域内既有极大值又有极小值,求实数 的取值范围;
的取值范围; ,使得当
,使得当 时,不等式
时,不等式 恒成立.
恒成立.
 的单调区间;
的单调区间; 时,不等式
时,不等式 恒成立,求实数
恒成立,求实数 的取值范围;
的取值范围; 的方程
的方程 在区间
在区间 上恰好有两个相异的实根,
上恰好有两个相异的实根, 的取值范围;
的取值范围;