题目内容
5.已知x为实数,用表示不超过x的最大整数,例如[1,2]=1,[-1.2]=-2,[1]=1,对于函数f(x),若存在m∈R且m∉Z,使得f(m)=f([m]),则称函数f(x)是Ω函数.(Ⅰ)判断函数f(x)=x2-$\frac{1}{3}$x,g(x)=sinπx是否是Ω函数;(只需写出结论)
(Ⅱ)设函数f(x)是定义R在上的周期函数,其最小正周期为T,若f(x)不是Ω函数,求T的最小值.
(Ⅲ)若函数f(x)=x+$\frac{a}{x}$是Ω函数,求a的取值范围.
分析 (Ⅰ)根据Ω函数的定义直接判断函数f(x)=x2-$\frac{1}{3}$x,g(x)=sinπx是否是Ω函数;
(Ⅱ)根据周期函数的定义,结合Ω函数的条件,进行判断和证明即可.
(Ⅲ)根据Ω函数的定义,分别讨论a=0,a<0和a>0时,满足的条件即可.
解答 解:(Ⅰ)f(x)=x2-$\frac{1}{3}$x是Ω函数,g(x)=sinπx不是Ω函数;------------------(4分)
(Ⅱ)T的最小值为1.--------------------------(11分)
因为f(x)是以T为最小正周期的周期函数,所以f(T)=f(0).
假设T<1,则[T]=0,所以f([T])=f(0),矛盾.--------------------------(6)
所以必有T≥1,
而函数l(x)=x-[x]的周期为1,且显然不是Ω函数,
综上,T的最小值为1.--------------------------(9分)
(Ⅲ) 当函数f(x)=x+$\frac{a}{x}$是Ω函数时,
若a=0,则f(x)=x显然不是Ω函数,矛盾.------(10分)
若a<0,则f′(x)=1-$\frac{a}{{x}^{2}}$>0,
所以f(x)在(-∞,0),(0,+∞)上单调递增,
此时不存在m<0,使得 f(m)=f([m]),
同理不存在m>0,使得 f(m)=f([m]),
又注意到m[m]≥0,即不会出现[m]<0<m的情形,
所以此时f(x)=x+$\frac{a}{x}$不是Ω函数.---------(11分)
当a>0时,设f(m)=f([m]),所以m+$\frac{a}{m}$=[m]+[$\frac{a}{m}$],所以有a=m[m],其中[m]≠0,
当m>0时,
因为[m]<m<[m]+1,所以[m]2<m[m]<([m]+1)[m],
所以[m]2<a<([m]+1)[m],--------(12分)
当m<0时,[m]<0,
因为[m]<m<[m]+1,所以[m]2>m[m]>([m]+1)[m],
所以[m]2>a>([m]+1)[m],--------(13分)
记k=[m],综上,我们可以得到
“a>0且?x∈N•,a≠k2且a≠k(k+1).------(14分)
点评 本题主要考查与周期函数有关的新定义试题,考查学生的运算和推理能力,综合性较强,有一定的难度.

| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
| A. | $\frac{2}{tanα}$ | B. | -$\frac{2}{tanα}$ | C. | $\frac{2}{sinα}$ | D. | -$\frac{2}{sinα}$ |
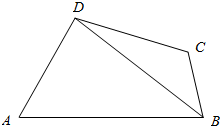 如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.
如图,在四边形ABCD中,AB=8,BC=3,CD=5,∠A=$\frac{π}{3}$,cos∠ADB=$\frac{1}{7}$.