题目内容
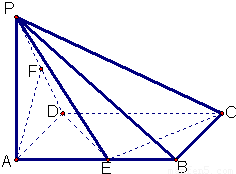
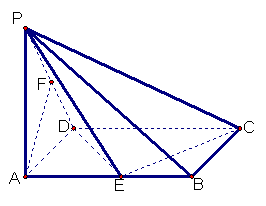 (13分)已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。
(13分)已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=1,AB=2,E、F分别是AB、PD的中点。
(Ⅰ)求证:AF∥平面PEC;
(Ⅱ)求PC与平面ABCD所成角的正切值;
(Ⅲ)求二面角P一EC一D的正切值。
解:(Ⅰ)取PC的中点O,连结OF、
OE.∴FO∥DC,且FO=![]() DC ∴FO∥AE
DC ∴FO∥AE
又E是AB的中点.且AB=DC.∴FO=AE.
∴四边形AEOF是平行四边形.∴AF∥OE 又OE![]() 平面PEC,AF
平面PEC,AF![]() 平面PEC ∴AF∥平面PEC
平面PEC ∴AF∥平面PEC
(Ⅱ)连结AC
∵PA⊥平面ABCD,∴∠PCA是直线PC与平
面ABCD所成的角
在Rt△PAC中,![]()
![]() 即直线PC与平面ABCD所成的角正切为
即直线PC与平面ABCD所成的角正切为![]()
(Ⅲ)作AM⊥CE,交CE的延长线于M.连结PM,由三垂线定理.得PM⊥CE∴∠PMA是二面角P—EC—D的平面角![]()
由△AME∽△CBE,可得![]() ,∴
,∴![]()
∴二面角P一EC一D的正切为![]()
解法二:以A为原点,如图建立直角坐标系,
则A(0.0,0),B(2,0,0),C(2,l,0),
D(0,1,0),F(0,![]() ,
,![]() ),E(1,0,0),
),E(1,0,0),
P(0,0,1)
(Ⅰ)取PC的中点O,连结OE,则O(1,![]() ,
,![]() ),
),
![]()
∴![]()
又OE![]() 平面PEC,AF
平面PEC,AF![]() 平面PEC,∴AF∥平面PEC
平面PEC,∴AF∥平面PEC
(Ⅱ)由题意可得![]() ,平面ABCD的法向量
,平面ABCD的法向量![]()
![]()
即直线PC与平面ABCD所成的角正切大小为![]() 。
。
(Ⅲ)设平面PEC的法向量为![]()
则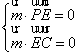 ,可得
,可得![]() ,令
,令![]() ,则
,则![]()
由(2)可得平面ABCD的法向量是![]()
![]()
∴二面角P一EC一D的正切大小为![]() 。
。

练习册系列答案
相关题目
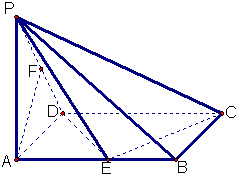 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
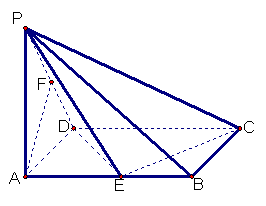
 已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,
已知在四棱锥P一ABCD中,底面ABCD是矩形,PA⊥平面ABCD,