题目内容
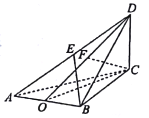
【题目】[2018·郴州期末]已知三棱锥![]() 中,
中,![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,
,![]() 是面积为
是面积为![]() 的等边三角形,
的等边三角形,![]() ,
,![]() ,
,![]() 平面
平面![]() ,垂足为
,垂足为![]() ,
,![]() 为线段
为线段![]() 的中点.
的中点.
(1)证明:![]() 平面
平面![]() ;
;
(2)求![]() 与平面
与平面![]() 所成的角的正弦值.
所成的角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:
(1)要证线面垂直,一般先证线线垂直,这可由![]() 和
和![]() 是等边三角形及O是AB中点易得;
是等边三角形及O是AB中点易得;
(2)要求直线与平面所成的角,一种方法作出线面角的平面角,然后解三角形得结论,也可建立空间直角坐标系,如解析中的坐标系,写出各点坐标,求出直线的方向向量与平面的法向量,由方向向量与法向量的夹角与直线和平面所成角互余可得.
试题解析:
(1)证明:∵![]() 垂直平分
垂直平分![]() ,垂足为
,垂足为![]() ,∴
,∴![]() .
.
∵![]() ,∴
,∴![]() 是等边三角形.
是等边三角形.
又![]() 是等边三角形.
是等边三角形.
∴![]() 是
是![]() 中点,
中点,![]() ,
,![]() .
.
∵![]() ,
,![]() ,
,![]() 平面
平面![]() ,∴
,∴![]() 平面
平面![]() .
.
(2)解:由(1)知![]() ,平面
,平面![]() 平面
平面![]() .
.
因为平面![]() 与平面
与平面![]() 的交线为
的交线为![]() .
.
∵![]() 平面
平面![]() .∴
.∴![]() .
.
又等边![]() 面积为
面积为![]() ,∴
,∴![]()
又![]() ,∴
,∴ ![]() 是
是![]() 中点.
中点.
如图建立空间直角坐标系![]() ,
,
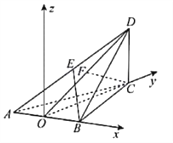
![]() ,
,![]() ,
,![]() ,
,![]()
所以![]() ,
,![]() ,
,![]()
设平面![]() 的法向量为
的法向量为![]() ,则
,则
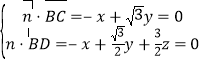 ,取
,取![]() ,则
,则![]() ,
,![]() .
.
即平面![]() 的一个法向量为
的一个法向量为![]() .
.
所以![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为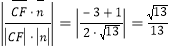 .
.

练习册系列答案
 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案
相关题目