题目内容
已知f(x)=x3-3x,若m2-4n>0,m,n∈R,求证:“2|m|+|n|<
解:由f(x)=x3-3x得f′(x)=3(x2-1),对x∈(-1,1)有f′(x)<0,故f(x)在(-1,1)上是减函数,得f(x)∈(-2,2).
于是“方程[f(x)]2+mf(x)+n=0在区间(-1,1)内有两个不等的实根”等价于“方程g(t)=t2+mt+n=0在区间(-2,2)内有两个不等的实根”.
所以“方程[f(x)]2+mf(x)+n=0在区间(-1,1)内有两个不等的实根”等价于
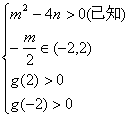
下面先证明充分性:由2|m|+|n|<4得|m|<4![]() -2<
-2<![]() <2,
<2,
且4>±
所以充分性成立.
下面再证不必要性:取m=2,n=![]() ,显然满足
,显然满足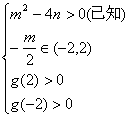
但是2|m|+|n|<4不成立,
即得不必要性成立.
综合以上得命题成立.

练习册系列答案
相关题目