题目内容
已知函数 (
(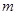 ,
,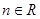 ,
,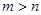 且
且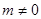 )的图象在
)的图象在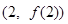 处的切线与
处的切线与 轴平行.
轴平行.
(1)确定实数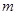 、
、 的正、负号;
的正、负号;
(2)若函数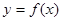 在区间
在区间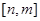 上有最大值为
上有最大值为 ,求
,求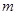 的值.
的值.
(1)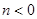 ,
, ;(2)
;(2) .
.
解析试题分析:(1)先求导数,因为切线与 轴平行,所以导数为0,列出等式,判断出
轴平行,所以导数为0,列出等式,判断出 的符号;(2)求导数,令导数为0,解出方程的根,利用导数的正负判断出函数的单调性,通过分类讨论的方法找到最大值,让最大值等于
的符号;(2)求导数,令导数为0,解出方程的根,利用导数的正负判断出函数的单调性,通过分类讨论的方法找到最大值,让最大值等于 ,解出
,解出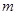 的值.
的值.
试题解析:(1)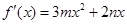 1分
1分
由图象在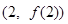 处的切线与
处的切线与 轴平行,
轴平行,
知 ,∴
,∴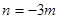 . 2分
. 2分
又 ,故
,故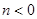 ,
, . 3分
. 3分
(2) 令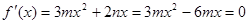 ,
,
得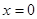 或
或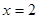 . 4分
. 4分
∵ ,令
,令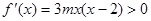 ,得
,得 或
或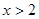
令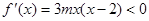 ,得
,得 .
.
于是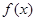 在区间
在区间 内为增函数,在
内为增函数,在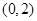 内为减函数,在
内为减函数,在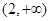 内为增函数.
内为增函数.
∴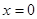 是
是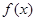 的极大值点,
的极大值点,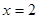 是极小值点. 5分
是极小值点. 5分
令 ,得
,得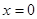 或
或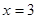 . 6分
. 6分
分类:① 当 时,
时, ,∴
,∴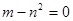 .
.
由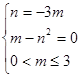 解得
解得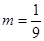 , 8分
, 8分
② 当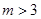 时,
时, , 9分
, 9分
∴ .
.
由 得
得  . 10分
. 10分
记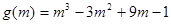 ,
,
∵ , 11分
, 11分
∴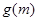 在
在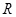 上是增函数,又
上是增函数,又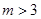 ,∴
,∴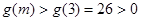 , 12分
, 12分
∴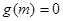 在
在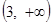 上无实数根. 13分
上无实数根. 13分
综上,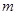 的值为
的值为 .
.

练习册系列答案
相关题目
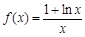 .
. 上存在极值,求实数
上存在极值,求实数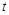 的取值范围;
的取值范围;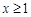 时,不等式
时,不等式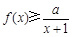 恒成立,求实数
恒成立,求实数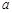 的取值范围.
的取值范围.
 求
求 在
在 处的切线方程;
处的切线方程; 上恰有两个零点,求
上恰有两个零点,求 的取值范围.
的取值范围. 排,在路南侧沿直线
排,在路南侧沿直线 排,现要在矩形区域
排,现要在矩形区域 内沿直线将
内沿直线将 ,
, ,公路两侧排管费用为每米1万元,穿过公路的
,公路两侧排管费用为每米1万元,穿过公路的 部分的排管费用为每米2万元,设
部分的排管费用为每米2万元,设 所成的小于
所成的小于 的角为
的角为 .
.
 关于
关于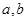 是实数,函数
是实数,函数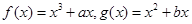 ,
,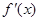 和
和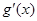 ,分别是
,分别是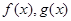 的导函数,若
的导函数,若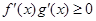 在区间
在区间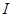 上恒成立,则称
上恒成立,则称 和
和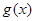 在区间
在区间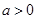 ,若函数
,若函数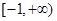 上单调性一致,求实数
上单调性一致,求实数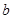 的取值范围;
的取值范围;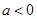 且
且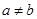 ,若函数
,若函数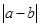 的最大值.
的最大值.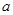 、
、 、
、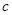 都是实数,函数
都是实数,函数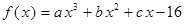 的导函数为
的导函数为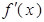 ,
,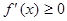 的解集为
的解集为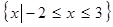 .
.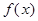 的极大值等于
的极大值等于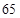 ,求
,求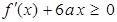 的解集为集合
的解集为集合 ,当
,当 时,函数
时,函数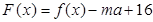 只有一个零点,求实数
只有一个零点,求实数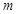 的取值范围.
的取值范围.
 上是减函数,求实数
上是减函数,求实数 的最小值;
的最小值; ,使
,使 (
( )成立,求实数
)成立,求实数 ,
, 为自然对数的底数).
为自然对数的底数).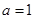 时,求
时,求 的单调区间;
的单调区间; 上无零点,求
上无零点,求 最小值;
最小值; ,在
,在 上总存在两个不同的
上总存在两个不同的
 ),使
),使 成立,求
成立,求
 时,判断函数
时,判断函数 是否有极值;
是否有极值; 时,
时, 上的增函数,求实数
上的增函数,求实数 的取值范围.
的取值范围.