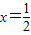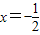Question

已知f（2x+1）是偶函数，则函数f（2x）图象的对称轴为（　　）

• A、x=1
• B、x=

  1

  2

• C、x=-

  1

  2

• D、x=-1

Answer 1

分析：根据复合函数的对称性，由f（2x+1）是偶函数，故函数f（2x+1）的图象关于Y轴对称，因为函数f（2x）图象可由f（2x+1）图象向右平移

1

2

个单位得到．从而得出函数f（2x）图象的对称轴．

解答：解：∵f（2x+1）是偶函数，
∴函数f（2x+1）的图象关于Y轴对称
因为函数f（2x）图象可由f（2x+1）图象向右平移

1

2

个单位得到．
∴函数f（2x）的图象关于直线x=

1

2

对称
故选B．

点评：本题主要考查了奇偶函数图象的对称性，求复合函数的对称轴的关键是“以不变应万变”，即不管函数括号里的式子形式怎么变化，可利用图象的变换得出其对称轴．