题目内容
求复合函数定义域.
(1)若f(x)定义域是[0,2],则f(2x-1)定义域是
(2)若f(x2-2x+2)定义域为[0,2],则f(x)定义域是
(3)已知f(2x-1)定义域为[-1,5],则f(2-5x)定义域是
(1)若f(x)定义域是[0,2],则f(2x-1)定义域是
[
,
]
| 1 |
| 2 |
| 3 |
| 2 |
[
,
]
| 1 |
| 2 |
| 3 |
| 2 |
(2)若f(x2-2x+2)定义域为[0,2],则f(x)定义域是
[1,2]
[1,2]
(3)已知f(2x-1)定义域为[-1,5],则f(2-5x)定义域是
[-
,1]
| 7 |
| 5 |
[-
,1]
.| 7 |
| 5 |
分析:(1)由于f(x)定义域是[0,2],令0≤2x-1≤2,求出x的范围,写成区间的形式即为f(2x-1)定义域
(2)由于f(x2-2x+2)的定义域为[0,2],求出x2-2x+2的值域即为(x)的定义域;
(3)由于f(2x-1)定义域为[-1,5],求出2x-1的值域,令2-5x在2x-1的值域内,求出x的范围写成区间的形式,即为f(2-5x)定义域;
(2)由于f(x2-2x+2)的定义域为[0,2],求出x2-2x+2的值域即为(x)的定义域;
(3)由于f(2x-1)定义域为[-1,5],求出2x-1的值域,令2-5x在2x-1的值域内,求出x的范围写成区间的形式,即为f(2-5x)定义域;
解答:解:(1)因为f(x)定义域是[0,2],
令0≤2x-1≤2,
解得
≤x≤
,
所以f(2x-1)定义域是 [
,
];
(2)因为f(x2-2x+2)的定义域为[0,2],
所以1≤x2-2x+2≤2,
所以f(x)的定义域为[1,2];
(3)因为f(2x-1)定义域为[-1,5],
所以-3≤2x-1≤9,
令-3≤2-5x≤9,
解得-
≤x≤1,
所以f(2-5x)定义域是[-
,1];
故答案为:[
,
];[1,2];[-
,1];
令0≤2x-1≤2,
解得
| 1 |
| 2 |
| 3 |
| 2 |
所以f(2x-1)定义域是 [
| 1 |
| 2 |
| 3 |
| 2 |
(2)因为f(x2-2x+2)的定义域为[0,2],
所以1≤x2-2x+2≤2,
所以f(x)的定义域为[1,2];
(3)因为f(2x-1)定义域为[-1,5],
所以-3≤2x-1≤9,
令-3≤2-5x≤9,
解得-
| 7 |
| 5 |
所以f(2-5x)定义域是[-
| 7 |
| 5 |
故答案为:[
| 1 |
| 2 |
| 3 |
| 2 |
| 7 |
| 5 |
点评:本题的考点是抽象函数的定义域的求法,由两种类型:①已知f(x)定义域为D,则f(g(x))的定义域是使g(x)∈D有意义的x的集合,②已知f(g(x))的定义域为D,则g(x)在D上的值域,即为f(x)定义域.

练习册系列答案
相关题目
 定义域是[0,2],则
定义域是[0,2],则 定义域是_____ __ _
定义域是_____ __ _ 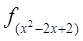 定义域为[0,2],则
定义域为[0,2],则 定义域是___
______
定义域是___
______ 定义域为[-1,5],则
定义域为[-1,5],则 定义域是___
___
定义域是___
___