题目内容
已知圆: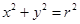 上任意一点
上任意一点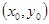 处的切线方程为:
处的切线方程为: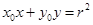 。类比以上结论有:双曲线:
。类比以上结论有:双曲线: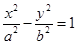 上任意一点
上任意一点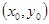 处的切线方程为:
处的切线方程为:
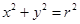 上任意一点
上任意一点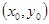 处的切线方程为:
处的切线方程为: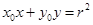 。类比以上结论有:双曲线:
。类比以上结论有:双曲线: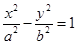 上任意一点
上任意一点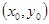 处的切线方程为:
处的切线方程为: 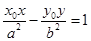
试题分析:因为圆:
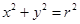 上任意一点
上任意一点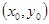 处的切线方程为:
处的切线方程为: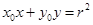 ,所以类比以上结论有:双曲线:
,所以类比以上结论有:双曲线: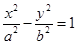 上任意一点
上任意一点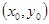 处的切线方程为:
处的切线方程为: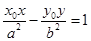 。
。点评:类比推理是特殊到特殊的推理。其一般步骤是:①找出两类事物之间的相似性或一致性;②用一类事物的性质去推测另一类事物的性质,得出一个明确的命题。

练习册系列答案
相关题目
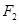 是双曲线
是双曲线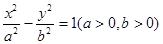 的左、右焦点,过
的左、右焦点,过 轴和双曲线右支于点
轴和双曲线右支于点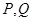 ,过
,过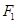 作直线
作直线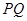 的垂线,垂足为
的垂线,垂足为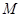 ,若
,若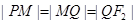 ,则双曲线的离心率为( )
,则双曲线的离心率为( )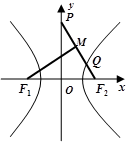
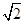
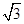
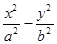 =1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为
=1(a>0,b>0)的一条渐近线与抛物线y=x2+1只有一个公共点,则双曲线的离心率为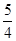
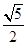
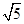
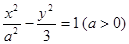 的离心率为
的离心率为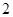 ,则双曲线的渐近线方程为
,则双曲线的渐近线方程为 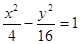 的渐近线
的渐近线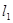 经过二、四象,直线
经过二、四象,直线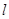 过点
过点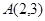 且垂直于直线
且垂直于直线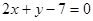
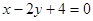

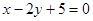
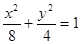 有相同的焦点,实半轴长为
有相同的焦点,实半轴长为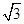 .
.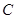 的方程;
的方程;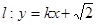 与双曲线
与双曲线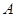 和
和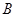 ,且
,且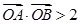
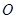 为原点),求
为原点),求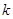 的取值范围.
的取值范围.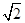
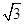
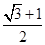
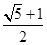
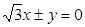 为渐近线,一个焦点坐标为
为渐近线,一个焦点坐标为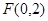 的双曲线方程是( )
的双曲线方程是( )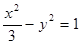
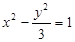
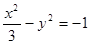
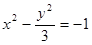
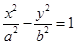 (a>0,b>0)上横坐标为
(a>0,b>0)上横坐标为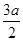 的点到右焦点的距离大于它到左准线的距离,则双曲线离心率的取值范围是( )
的点到右焦点的距离大于它到左准线的距离,则双曲线离心率的取值范围是( ) )
)