题目内容
（2011•西安模拟）设不等式组
所表示的平面区域为S，若A、B为S内的任意两个点，则|AB|的最大值为
．
|
| 65 |
| 65 |
分析：欲求对应的平面区域图形，先由线性约束条件画出区域，它是一个梯形，欲求|AB|的最大值，观察平面区域知，D、F两点距离最大，故只要求出此两点的距离即得．
解答：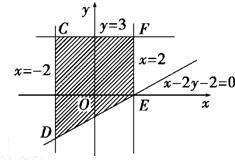
解：原不等式组可以化为
，
画出对应的平面区域图形如图所示的阴影部分．
它是一个直角梯形，
且坐标依次为E（2，0），F（2，3），C（-2，3），D（-2，-2）．
显然在平面区域内，D、F两点距离最大为
，
即|AB|的最大值为
．
故答案为：
．
解：原不等式组可以化为
|
画出对应的平面区域图形如图所示的阴影部分．
它是一个直角梯形，
且坐标依次为E（2，0），F（2，3），C（-2，3），D（-2，-2）．
显然在平面区域内，D、F两点距离最大为
| 65 |
即|AB|的最大值为
| 65 |
故答案为：
| 65 |
点评：本题只是直接考查线性规划问题，是一道较为简单的送分题．近年来高考线性规划问题高考数学考试的热点，数形结合是数学思想的重要手段之一，是连接代数和几何的重要方法．随着要求数学知识从书本到实际生活的呼声不断升高，线性规划这一类新型数学应用问题要引起重视．
练习册系列答案
相关题目
