题目内容
已知椭圆 的方程为
的方程为 双曲线
双曲线 的两条渐近线为
的两条渐近线为 和
和 ,过椭圆
,过椭圆 的右焦点
的右焦点 作直线
作直线 ,使得
,使得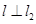 于点
于点 ,又
,又 与
与 交于点
交于点 ,
, 与椭圆
与椭圆 的两个交点从上到下依次为
的两个交点从上到下依次为 (如图).
(如图).
(1)当直线 的倾斜角为
的倾斜角为 ,双曲线的焦距为8时,求椭圆的方程;
,双曲线的焦距为8时,求椭圆的方程;
(2)设 ,证明:
,证明: 为常数.
为常数.

【答案】
解:(1)由已知, ,
,
解得: ,
,
 所以椭圆
所以椭圆 的方程是:
的方程是: .
.
(2)解法1:设
由题意得: 直线 的方程为:
的方程为:  ,直线
,直线 的方程为:
的方程为:  ,
,
则直线 的方程为:
的方程为:  ,其中点
,其中点 的坐标为
的坐标为 ;
;

 由
由  得:
得:  ,则点
,则点 ;
;
 由
由 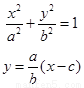 消y得:
消y得: ,则
,则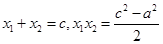 ;
;
由 得:
得: ,则:
,则: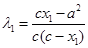 ,
,
同理由 得:
得: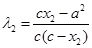 ,
,

故 为常数.
为常数.
【解析】略

练习册系列答案
相关题目
 +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B). +
+ =1,(a>b>0)与双曲4x2-
=1,(a>b>0)与双曲4x2- y2=1有相同的焦点,且椭C的离心e=
y2=1有相同的焦点,且椭C的离心e= ,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).
,又A,B为椭圆的左右顶点,M为椭圆上任一点(异于A,B).