题目内容
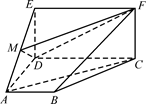
如图,四边形ABCD是梯形,四边形CDEF是矩形,且平面ABCD⊥平面CDEF,∠BAD=∠CDA=90°,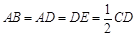 ,M是线段AE上的动点.
,M是线段AE上的动点.
(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.
 ,M是线段AE上的动点.
,M是线段AE上的动点.(1)试确定点M的位置,使AC∥平面DMF,并说明理由;
(2)在(1)的条件下,求平面DMF与平面ABCD所成锐二面角的余弦值.

(1)详见解析;(2)所求二面角的余弦值为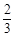 .
.
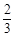 .
.试题分析:(1)要使得AC∥平面DMF,需要使得AC平行平面DMF内的一条直线.为了找这条直线,需要作一个过AC而与平面DMF相交的平面.为此,连结CE,交DF于N,连结MN,这样只要AC∥MN即可.因为N为线段DF的中点,所以只需M是线段AE的中点即可.
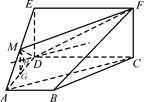
(2)思路一、(综合法)首先作出它们的交线.过点D作平面DMF与平面ABCD的交线l,由于AC∥平面DMF,由线面平行的性质定理知AC∥l.为了求二面角,首先作出其平面角.作平面角第一步是过其中一个面内一点作另一个面的垂线,而要作垂线先作垂面.在本题中,由于平面
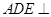 平面
平面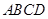 ,所以过点M作MG⊥AD于G,因为平面ABCD⊥平面CDEF,DE⊥CD,所以DE⊥平面ABCD,则平面ADE⊥平面ABCD,所以MG⊥平面ABCD,过G作GH⊥l于H,连结MH,则直线l⊥平面MGH,所以l⊥MH,故∠MHG是平面MDF与平面ABCD所成锐二面角的平面角.在直角三角形MHG中求得可∠MHG的余弦值.(另外也可过点C作直线l的垂线)思路二、因为平面ABCD⊥平面CDEF,DE⊥CD,所以DE⊥平面ABCD,可知AD,CD,DE两两垂直,所以可分别以
,所以过点M作MG⊥AD于G,因为平面ABCD⊥平面CDEF,DE⊥CD,所以DE⊥平面ABCD,则平面ADE⊥平面ABCD,所以MG⊥平面ABCD,过G作GH⊥l于H,连结MH,则直线l⊥平面MGH,所以l⊥MH,故∠MHG是平面MDF与平面ABCD所成锐二面角的平面角.在直角三角形MHG中求得可∠MHG的余弦值.(另外也可过点C作直线l的垂线)思路二、因为平面ABCD⊥平面CDEF,DE⊥CD,所以DE⊥平面ABCD,可知AD,CD,DE两两垂直,所以可分别以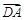 ,
,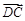 ,
,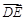 的方向为x,y,z轴,建立空间直角坐标系O-xyz.然后利用空间向量求解.
的方向为x,y,z轴,建立空间直角坐标系O-xyz.然后利用空间向量求解. (1)当M是线段AE的中点时,AC∥平面DMF.
证明如下:
连结CE,交DF于N,连结MN,
由于M、N分别是AE、CE的中点,所以MN∥AC,
由于MN
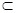 平面DMF,又AC
平面DMF,又AC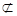 平面DMF,
平面DMF,所以AC∥平面DMF. 4分
(2)方法一、过点D作平面DMF与平面ABCD的交线l,由于AC∥平面DMF,可知AC∥l,
过点M作MG⊥AD于G,
因为平面ABCD⊥平面CDEF,DE⊥CD,
所以DE⊥平面ABCD,则平面ADE⊥平面ABCD,
所以MG⊥平面ABCD,
过G作GH⊥l于H,连结MH,则直线l⊥平面MGH,所以l⊥MH,
故∠MHG是平面MDF与平面ABCD所成锐二面角的平面角. 8分
设
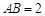 ,则
,则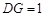 ,
,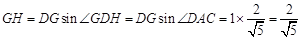 ,
,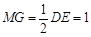 ,则
,则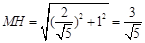 , 11分
, 11分所以
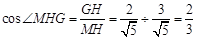 ,即所求二面角的余弦值为
,即所求二面角的余弦值为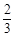 . 12分
. 12分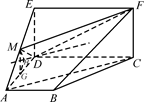
方法二、因为平面ABCD⊥平面CDEF,DE⊥CD,所以DE⊥平面ABCD,可知AD,CD,DE两两垂直,分别以
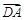 ,
,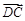 ,
,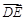 的方向为x,y,z轴,建立空间直角坐标系O-xyz.
的方向为x,y,z轴,建立空间直角坐标系O-xyz.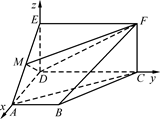
设
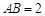 ,则
,则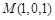 ,
,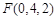 ,
,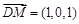 ,
,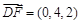 ,
,设平面MDF的法向量
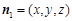 ,
,则
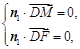 所以
所以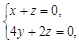
令
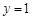 ,得平面MDF的一个法向量
,得平面MDF的一个法向量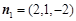 , 8分
, 8分取平面ABCD的法向量
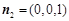 , 9分
, 9分由
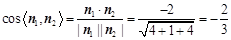 , 11分
, 11分故平面MDF与平面ABCD所成锐二面角的余弦值为
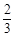 . 12分
. 12分
练习册系列答案
相关题目
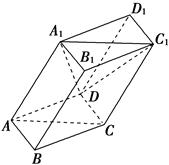
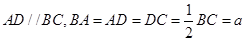 ,E是BC的中点,将△BAE沿AE翻折成
,E是BC的中点,将△BAE沿AE翻折成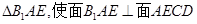 ,F为
,F为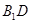 的中点.
的中点.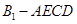 的体积;
的体积;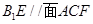 ;
; 所成锐二面角的余弦值.
所成锐二面角的余弦值.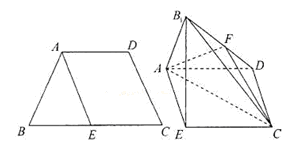
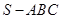 中,
中,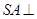 底面
底面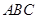 ,点
,点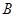 为以
为以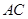 为直径的圆上任意一动点,且
为直径的圆上任意一动点,且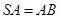 ,点
,点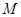 是
是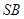 的中点,
的中点,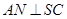 且交
且交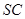 于点
于点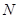 .
.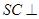 面
面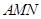 ;
;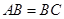 时,求二面角
时,求二面角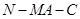 的余弦值.
的余弦值.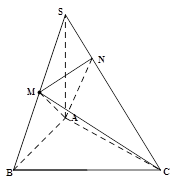
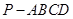 的底面的菱形,
的底面的菱形,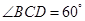 ,点
,点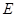 是
是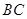 边的中点,
边的中点,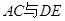 交于点
交于点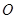 ,
,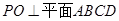
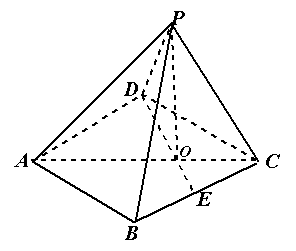
 ;
;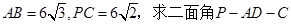 的大小;
的大小;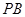 与
与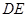 所成角的余弦值。
所成角的余弦值。
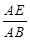 的值;
的值; AB.
AB.