题目内容
已知函数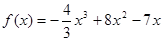
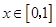
(Ⅰ)求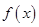 的单调区间和值域;
的单调区间和值域;
(Ⅱ)设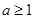 ,函数
,函数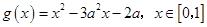 ,若对于任意
,若对于任意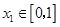 ,总存在
,总存在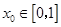 ,
,
使得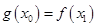 成立,求
成立,求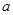 的取值范围
的取值范围
【答案】
(1)当 时,
时, 是减函数;当
是减函数;当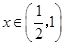 时,
时, 是增函数;
是增函数;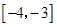
(2)
【解析】对函数 求导,得
求导,得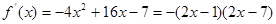
令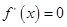 解得
解得 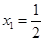 或
或
|
x[来源:ZXXK] |
0 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
当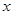 变化时,
变化时, 、
、 的变化情况如右表:
的变化情况如右表:
所以,当 时,
时, 是减函数;当
是减函数;当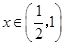 时,
时, 是增函数;
是增函数;
当 时,
时, 的值域为
的值域为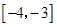
(Ⅱ)对函数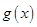 求导,得
求导,得 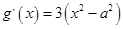
因此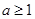 ,当
,当 时,
时, 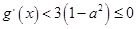 中学[来源:Z_xx_k.Com]
中学[来源:Z_xx_k.Com]
因此当 时,
时,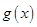 为减函数,从而当
为减函数,从而当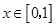 时有
时有
又 ,
, ,即当
,即当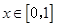 时有
时有
任给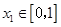 ,
,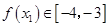 ,存在
,存在 使得
使得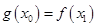 ,则中学
,则中学
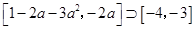 即
即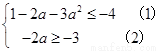 解
解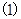 式得
式得 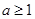 或
或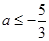
解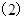 式得
式得 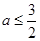 又
又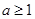 ,故:
,故: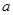 的取值范围为
的取值范围为

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
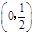
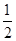
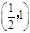
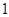
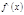


 [来源:学_科_网Z_X_X_K]
[来源:学_科_网Z_X_X_K]


 .
. 上的最大值和最小值.
上的最大值和最小值. .
. 成立的
成立的 的取值范围;
的取值范围; 时,求函数
时,求函数 的值域.
的值域. .
. 的单调区间;
的单调区间; 个单位得到函数
个单位得到函数 ,求
,求 在区间
在区间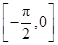 上的最小值和最大值.
上的最小值和最大值. .
. 的最小正周期及最值;
的最小正周期及最值; ,判断函数
,判断函数 的奇偶性,并说明理由.
的奇偶性,并说明理由.