题目内容
已知函数 .
.(Ⅰ)求f(x)的最小正周期:
(Ⅱ)求f(x)在区间
 上的最大值和最小值.
上的最大值和最小值.
【答案】分析:(Ⅰ)利用两角和公式和二倍角公式对函数的解析式进行化简整理后,利用正弦函数的性质求得函数的最小正周期.
(Ⅱ)利用x的范围确定2x+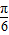 的范围,进而利用正弦函数的单调性求得函数的最大和最小值.
的范围,进而利用正弦函数的单调性求得函数的最大和最小值.
解答:解:(Ⅰ)∵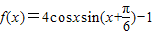
=4cosx(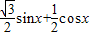 )-1
)-1
=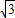 sin2x+2cos2x-1
sin2x+2cos2x-1
=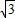 sin2x+cos2x
sin2x+cos2x
=2sin(2x+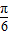 )
)
所以函数的最小正周期为π
(Ⅱ)∵-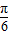 ≤x≤
≤x≤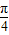 ,
,
∴-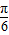 ≤2x+
≤2x+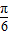 ≤
≤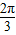
∴当2x+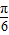 =
=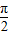 ,即x=
,即x=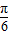 时,f(x)取最大值2
时,f(x)取最大值2
当2x+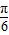 =-
=-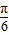 时,即x=-
时,即x=-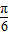 时,f(x)取得最小值-1
时,f(x)取得最小值-1
点评:本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.
(Ⅱ)利用x的范围确定2x+
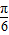 的范围,进而利用正弦函数的单调性求得函数的最大和最小值.
的范围,进而利用正弦函数的单调性求得函数的最大和最小值.解答:解:(Ⅰ)∵
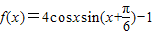
=4cosx(
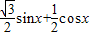 )-1
)-1=
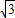 sin2x+2cos2x-1
sin2x+2cos2x-1=
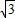 sin2x+cos2x
sin2x+cos2x=2sin(2x+
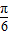 )
)所以函数的最小正周期为π
(Ⅱ)∵-
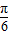 ≤x≤
≤x≤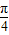 ,
,∴-
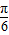 ≤2x+
≤2x+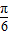 ≤
≤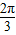
∴当2x+
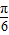 =
=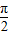 ,即x=
,即x=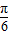 时,f(x)取最大值2
时,f(x)取最大值2当2x+
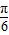 =-
=-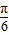 时,即x=-
时,即x=-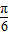 时,f(x)取得最小值-1
时,f(x)取得最小值-1点评:本题主要考查了三角函数的周期性及其求法,三角函数的最值.解题的关键是对函数解析式的化简整理.

练习册系列答案
相关题目
 .
. .
. 个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值.
个单位,得到函数g(x)的图象,求函数g(x)在区间[0,π]上的最大值和最小值. .
. 上恒成立,求实数m的取值范围.
上恒成立,求实数m的取值范围. .
. 成等差数列,且
成等差数列,且 =9,求a的值.
=9,求a的值. .
.