题目内容
给出下列命题:
①在△ABC中,若
•
>0,则△ABC是钝角三角形;
②在△ABC中,若cosA•tanB•cotC<0,则△ABC是钝角三角形;
③在△ABC中,若sinA•sinB<cosA•cosB,则△ABC是钝角三角形;
④在△ABC中,若acosA=bcosB,则△ABC是等腰三角形.
其中正确的命题序号是
①在△ABC中,若
| AB |
| BC |
②在△ABC中,若cosA•tanB•cotC<0,则△ABC是钝角三角形;
③在△ABC中,若sinA•sinB<cosA•cosB,则△ABC是钝角三角形;
④在△ABC中,若acosA=bcosB,则△ABC是等腰三角形.
其中正确的命题序号是
①②③
①②③
.分析:利用向量的数量积与实际意义可判断①的正误,利用三角函数的性质与诱导公式可判断②,利用两角和的余弦可判断③,利用正弦定理与正、余弦的二倍角公式可判断④.
解答:解:对于①,∵在△ABC中,
•
=cbcos(π-B)>0,
∴cosB<0,
∴B为钝角,即△ABC是钝角三角形,①正确;
对于②,在△ABC中,cosA•tanB•cotC<0,则A、B、C中必有一角为钝角,故②正确;
对于③,在△ABC中,sinA•sinB<cosA•cosB?cos(A+B)>0?cosC<0,
故C为钝角,即△ABC是钝角三角形,③正确;
对于④,由正弦定理可得sinAcosA=sinBcosB?
sin2A=
sin2B,
∴A=B或2A=π-2B,
∴△ABC是等腰三角形或直角三角形,故④错误.
故答案为:①②③
| AB |
| BC |
∴cosB<0,
∴B为钝角,即△ABC是钝角三角形,①正确;
对于②,在△ABC中,cosA•tanB•cotC<0,则A、B、C中必有一角为钝角,故②正确;
对于③,在△ABC中,sinA•sinB<cosA•cosB?cos(A+B)>0?cosC<0,
故C为钝角,即△ABC是钝角三角形,③正确;
对于④,由正弦定理可得sinAcosA=sinBcosB?
| 1 |
| 2 |
| 1 |
| 2 |
∴A=B或2A=π-2B,
∴△ABC是等腰三角形或直角三角形,故④错误.
故答案为:①②③
点评:本题考查三角形的形状判断,考查向量的数量积,考查两角和的余弦与二倍角公式,考查正弦定理及三角函数的性质与诱导公式,属于三角与向量的综合,属于中档题.

练习册系列答案
相关题目
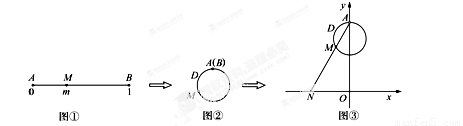
 到实数集R的映射过程:区间
到实数集R的映射过程:区间 围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为
围成一个圆,使两端点A、B恰好重合,如图②;再将这个圆放在平面直角坐标系中,使其圆心在y轴上,点A的坐标为 ,则m的象就是n,记作
,则m的象就是n,记作 .
.
 ;
; 在定义域
在定义域 上单调递增;
上单调递增; ;
; 的不等式
的不等式 的解集为
的解集为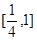 .
.
 ”的否命题为“若
”的否命题为“若 ”
” ”的否定是“
”的否定是“ ”
”