题目内容
已知函数f(x)=ln(ex+a)(a>0).
(1)求函数y=f(x)的反函数y=f-1(x)及f(x)的导数f′(x);
(2)假设对任意x∈[ln(3a),ln(4a)],不等式|m-f-1(x)|+ln(f′(x))<0成立,求实
数m的取值范围.
解:(1)、设y=ln(ex+a),a>0,则ey=ex+a,∴ex=ey-a,a>0,∴x=ln(ey-a),x,y互换得到函数y=f(x)的反函数f-1(x)=ln(ex-a),x∈R;f′(x)=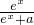 .
.
(2)、由|m-f-1(x)|+ln(f'(x))<0得ln(ex-a)-ln(ex+a)+x<m<ln(ex-a)+ln(ex+a)-x.
设?(x)=ln(ex-a)-ln(ex+a)+x,ψ(x)=ln(ex-a)+ln(ex+a)-x,
于是原不等式对于x∈[ln(3a),ln(4a)]恒成立等价于?(x)<m<ψ(x).
由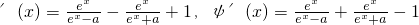 ,注意到0<ex-a<ex<ex+a,故有?'(x)>0,ψ'(x)>0,从而可?(x)与?(x)均在[ln(3a),ln(4a)]上单调递增,因此不等式?(x)<m<ψ(x)成立当且仅当?(ln(4a))<m<ψ(ln(3a)).即
,注意到0<ex-a<ex<ex+a,故有?'(x)>0,ψ'(x)>0,从而可?(x)与?(x)均在[ln(3a),ln(4a)]上单调递增,因此不等式?(x)<m<ψ(x)成立当且仅当?(ln(4a))<m<ψ(ln(3a)).即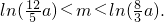
分析:(1)、设y=ln(ex+a),a>0,把y看作常数,解出x后把x,y互换就得到函数y=f(x)的反函数f-1(x).再由复合函数的求解法则解出f(x)的导数f′(x).
(2)、由|m-f-1(x)|+ln(f'(x))<0得ln(ex-a)-ln(ex+a)+x<m<ln(ex-a)+ln(ex+a)-x.原不等式对于x∈[ln(3a),ln(4a)]恒成立等价于ln(ex-a)-ln(ex+a)+x<ln(ex-a)+ln(ex+a)-x.再通过导数运算和函数的单调性求出实数m的取值范围.
点评:本题是对数函数、反函数和导数的综合应用题,考查反函数和复合函数的求导,具有一定的难度.在解题时要注意转化思想的灵活运用.
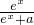 .
.(2)、由|m-f-1(x)|+ln(f'(x))<0得ln(ex-a)-ln(ex+a)+x<m<ln(ex-a)+ln(ex+a)-x.
设?(x)=ln(ex-a)-ln(ex+a)+x,ψ(x)=ln(ex-a)+ln(ex+a)-x,
于是原不等式对于x∈[ln(3a),ln(4a)]恒成立等价于?(x)<m<ψ(x).
由
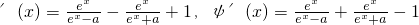 ,注意到0<ex-a<ex<ex+a,故有?'(x)>0,ψ'(x)>0,从而可?(x)与?(x)均在[ln(3a),ln(4a)]上单调递增,因此不等式?(x)<m<ψ(x)成立当且仅当?(ln(4a))<m<ψ(ln(3a)).即
,注意到0<ex-a<ex<ex+a,故有?'(x)>0,ψ'(x)>0,从而可?(x)与?(x)均在[ln(3a),ln(4a)]上单调递增,因此不等式?(x)<m<ψ(x)成立当且仅当?(ln(4a))<m<ψ(ln(3a)).即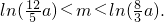
分析:(1)、设y=ln(ex+a),a>0,把y看作常数,解出x后把x,y互换就得到函数y=f(x)的反函数f-1(x).再由复合函数的求解法则解出f(x)的导数f′(x).
(2)、由|m-f-1(x)|+ln(f'(x))<0得ln(ex-a)-ln(ex+a)+x<m<ln(ex-a)+ln(ex+a)-x.原不等式对于x∈[ln(3a),ln(4a)]恒成立等价于ln(ex-a)-ln(ex+a)+x<ln(ex-a)+ln(ex+a)-x.再通过导数运算和函数的单调性求出实数m的取值范围.
点评:本题是对数函数、反函数和导数的综合应用题,考查反函数和复合函数的求导,具有一定的难度.在解题时要注意转化思想的灵活运用.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目