题目内容
(12分)如图,三条直线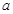 、
、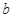 、
、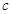 两两平行,直线
两两平行,直线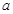 、
、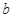 间的距离为
间的距离为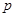 ,直线
,直线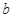 、
、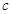 间的距离为
间的距离为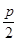 ,
,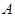 、
、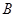 为直线
为直线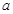 上的两个定点,且
上的两个定点,且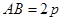 ,
,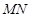 是在直线
是在直线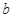 上滑动的长度为
上滑动的长度为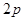 的线段.
的线段.
(1)建立适当的平面直角坐标系,求△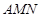 的外心
的外心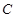 的轨迹
的轨迹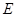 ;
;
(2)当△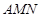 的外心
的外心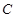 在
在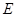 上什么位置时,使
上什么位置时,使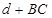 最小?最小值是多少?(其中,
最小?最小值是多少?(其中,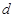 为外心
为外心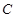 到直线
到直线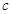 的距离)
的距离)
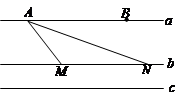
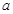 、
、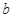 、
、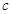 两两平行,直线
两两平行,直线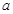 、
、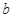 间的距离为
间的距离为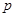 ,直线
,直线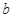 、
、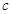 间的距离为
间的距离为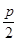 ,
,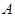 、
、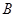 为直线
为直线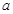 上的两个定点,且
上的两个定点,且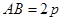 ,
,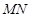 是在直线
是在直线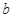 上滑动的长度为
上滑动的长度为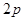 的线段.
的线段.(1)建立适当的平面直角坐标系,求△
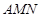 的外心
的外心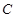 的轨迹
的轨迹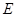 ;
;(2)当△
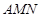 的外心
的外心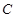 在
在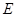 上什么位置时,使
上什么位置时,使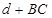 最小?最小值是多少?(其中,
最小?最小值是多少?(其中,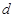 为外心
为外心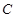 到直线
到直线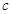 的距离)
的距离)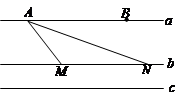
解:(1)以直线b为x轴,以过点A且与b直线垂直的直线为y轴建立平面直角坐标系,则由题意有A(0, p),设△AMN的外心坐标为C(x, y),则M(x – p,0),N(x+p, 0),
由题意有|CA|="|CM|." ∴
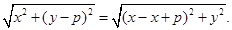
化简,得x2=2py,它是以原点为顶点、y轴为对称轴、开口向上的抛物线.
(2)不难知道,直线c恰为轨迹E的准线,由抛物线的定义知,d=|CF|,其中
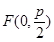 是抛物线的焦点. ∴d+|BC|=|CF|+|BC|.
是抛物线的焦点. ∴d+|BC|=|CF|+|BC|.由两点间直线段最短知,线段BF与轨迹E的交点即为所求的使d+|BC|最小的点.
由两点式方程可求得直线BF的方程为
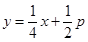 ,
,把它与x2=2py联立,得
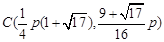 .
. 故当△AMN外心C为
 时,d+BC最小. 最小值
时,d+BC最小. 最小值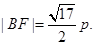
略

练习册系列答案
相关题目
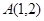 且与直线
且与直线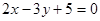 垂直的直线方程为 ( )
垂直的直线方程为 ( )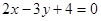
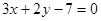
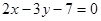
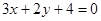
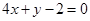 平行;
平行;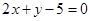 垂直.
垂直.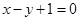
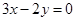
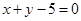
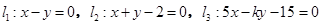 构成一个三角形,则
构成一个三角形,则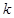 的取值范围是( )
的取值范围是( )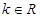
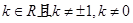
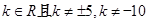
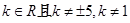
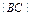
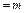 ,当三个角满足条件
,当三个角满足条件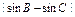
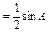 时,求A的轨迹方程
时,求A的轨迹方程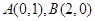 的直线的方程为 .
的直线的方程为 .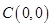 距离为
距离为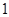 ,且与点
,且与点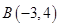 距离为
距离为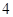 的直线条数共有 条.
的直线条数共有 条.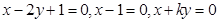 ,如果这三条直线将平面划分为六部分,则实数
,如果这三条直线将平面划分为六部分,则实数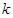 的取值集合为
的取值集合为