题目内容
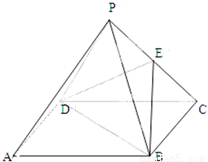
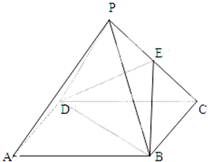 如图,已知在正四棱锥P-ABCD中,E是PC的中点
如图,已知在正四棱锥P-ABCD中,E是PC的中点求证:(1)PA∥平面BDE;
(2)平面BDE⊥平面PAC.
分析:(1)在平面内作已知直线的平行线,利用线线平行证线面平行即可.
(2)根据面面垂直的判定定理,先证线面垂直,再由线面垂直证明面面垂直.
(2)根据面面垂直的判定定理,先证线面垂直,再由线面垂直证明面面垂直.
解答: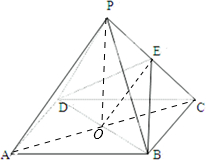 证明:(1)连接AC,交BD于O,连接OE,
证明:(1)连接AC,交BD于O,连接OE,
∵正四棱锥P-ABCD,∴O是AC的中点,
又E是PC的中点,∴OE∥PA,
OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE.
(2)连接OP,∵正四棱锥P-ABCD,∴AC⊥BD,OP⊥BD,
又∵AC∩PO=O,AC、PO?平面PAC,∴BD⊥平面PAC,
又BD?平面BDE,
∴平面BDE⊥平面PAC.
 证明:(1)连接AC,交BD于O,连接OE,
证明:(1)连接AC,交BD于O,连接OE,∵正四棱锥P-ABCD,∴O是AC的中点,
又E是PC的中点,∴OE∥PA,
OE?平面BDE,PA?平面BDE,
∴PA∥平面BDE.
(2)连接OP,∵正四棱锥P-ABCD,∴AC⊥BD,OP⊥BD,
又∵AC∩PO=O,AC、PO?平面PAC,∴BD⊥平面PAC,
又BD?平面BDE,
∴平面BDE⊥平面PAC.
点评:本题考查线面平行的判定及面面垂直的判定.

练习册系列答案
 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案
相关题目
 (2012•杨浦区一模)已知在正四棱锥P-ABCD中(如图),高为1cm,其体积为4cm3,求异面直线PA与CD所成角的大小.
(2012•杨浦区一模)已知在正四棱锥P-ABCD中(如图),高为1cm,其体积为4cm3,求异面直线PA与CD所成角的大小. -
- 中(如图),高为1
中(如图),高为1  ,其体积为4
,其体积为4  ,求异面直线
,求异面直线 与
与 所成角的大小.
所成角的大小.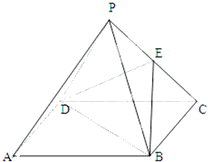 如图,已知在正四棱锥P-ABCD中,E是PC的中点
如图,已知在正四棱锥P-ABCD中,E是PC的中点