题目内容
 (2012•杨浦区一模)已知在正四棱锥P-ABCD中(如图),高为1cm,其体积为4cm3,求异面直线PA与CD所成角的大小.
(2012•杨浦区一模)已知在正四棱锥P-ABCD中(如图),高为1cm,其体积为4cm3,求异面直线PA与CD所成角的大小.分析:连接AC、BD交于O点,连接PO.根据锥体体积公式,结合题中数据可算出正四棱锥的底面边长,从而用勾股定理算出PA长,然后在△PAB中,利用余弦定理计算出∠PAB的余弦值,因为CD∥AB,所以这个余弦值就是PA与CD所成角θ的余弦值,从而得到异面直线PA与CD所成角的大小.
解答:解:连接AC、BD交于O点,连接PO,则PO就是正四棱锥的高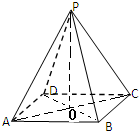
设异面直线PA与CD所成角的大小θ,底边长为a,
则依题意得,正四棱锥P-ABCD体积为V=
a2×1=4 …(4分)
∴a=2
,可得AC=2
Rt△PAO中,OA=
,PO=1
∴PA=
=
…(7分)
因为CD∥AB,所以直线PA与AB所成的锐角就是PA与CD所成角θ. …(9分)
△PAB中,PA=PB=
,AB=2
,
∴cos∠PAB=
=
,即cosθ=
,
所以PA与CD所成角θ=arccos
. …(12分)

设异面直线PA与CD所成角的大小θ,底边长为a,
则依题意得,正四棱锥P-ABCD体积为V=
| 1 |
| 3 |
∴a=2
| 3 |
| 6 |
Rt△PAO中,OA=
| 6 |
∴PA=
12+(
|
| 7 |
因为CD∥AB,所以直线PA与AB所成的锐角就是PA与CD所成角θ. …(9分)
△PAB中,PA=PB=
| 7 |
| 3 |
∴cos∠PAB=
| 7+12-7 | ||||
2×
|
| ||
| 7 |
| ||
| 7 |
所以PA与CD所成角θ=arccos
| ||
| 7 |
点评:本题给出一个正四面体,叫我们求异面直线所成角,着重考查了正棱锥的性质、余弦定理和异面直线所成角的求法等知识,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目