题目内容
已知命题p:f(x)=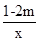 在区间(0,+∞)上是减函数;命题q:不等式(x-1)2>m的解集为R.若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围是。
在区间(0,+∞)上是减函数;命题q:不等式(x-1)2>m的解集为R.若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围是。
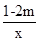 在区间(0,+∞)上是减函数;命题q:不等式(x-1)2>m的解集为R.若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围是。
在区间(0,+∞)上是减函数;命题q:不等式(x-1)2>m的解集为R.若命题“p∨q”为真,命题“p∧q”为假,求实数m的取值范围是。0≤m<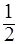 .
.
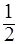 .
.本试题主要是考查了函数的单调性和不等式的求解的综合运用,以及复合命题的真值的运用。
由f(x)=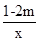 在区间(0,+∞)上是减函数,得1-2m>0,即m<
在区间(0,+∞)上是减函数,得1-2m>0,即m<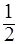
由不等式(x-1)2>m的解集为R,得m<0.,再结合命题“p∨q”为真,命题“p∧q”为假,说明一真一假,讨论得到。
解:由f(x)=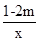 在区间(0,+∞)上是减函数,得1-2m>0,即m<
在区间(0,+∞)上是减函数,得1-2m>0,即m<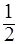 ,由不等式(x-1)2>m的解集为R,得m<0.要保证命题“p∨q”为真,命题“p∧q”为假,则需要两个命题中只有一个正确,而另一个不正确,
,由不等式(x-1)2>m的解集为R,得m<0.要保证命题“p∨q”为真,命题“p∧q”为假,则需要两个命题中只有一个正确,而另一个不正确,
故0≤m<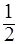 .
.
由f(x)=
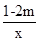 在区间(0,+∞)上是减函数,得1-2m>0,即m<
在区间(0,+∞)上是减函数,得1-2m>0,即m<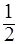
由不等式(x-1)2>m的解集为R,得m<0.,再结合命题“p∨q”为真,命题“p∧q”为假,说明一真一假,讨论得到。
解:由f(x)=
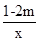 在区间(0,+∞)上是减函数,得1-2m>0,即m<
在区间(0,+∞)上是减函数,得1-2m>0,即m<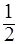 ,由不等式(x-1)2>m的解集为R,得m<0.要保证命题“p∨q”为真,命题“p∧q”为假,则需要两个命题中只有一个正确,而另一个不正确,
,由不等式(x-1)2>m的解集为R,得m<0.要保证命题“p∨q”为真,命题“p∧q”为假,则需要两个命题中只有一个正确,而另一个不正确,故0≤m<
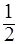 .
.
练习册系列答案
 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案
相关题目
 ,命题
,命题 :
: 在区间
在区间 上为减函数;命题
上为减函数;命题 :方程
:方程 在
在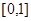 有解。若
有解。若 为真,
为真, 为假,求实数
为假,求实数 的取值范围。
的取值范围。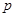 :对
:对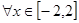 ,函数
,函数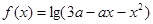 总有意义;
总有意义;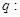 函数
函数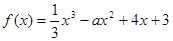 在
在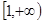 上是增函数;若命题“
上是增函数;若命题“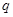 ”为真,求
”为真,求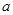 的取值范围。
的取值范围。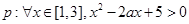 是假命题,则实数
是假命题,则实数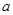 的取值范围是
的取值范围是  :关于
:关于 的不等式
的不等式 对于一切
对于一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围;
的取值范围; 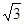 }没有极限; ②数列{(-1)n
}没有极限; ②数列{(-1)n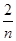 }的极限为0;
}的极限为0;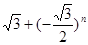 }的极限为
}的极限为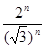 }没有极限.
}没有极限.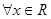 ,
, 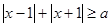 都成立,则实数
都成立,则实数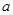 的取值范围是( )
的取值范围是( )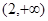
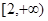
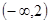
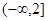
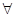 x1,x2
x1,x2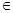 R,(f(x2)
R,(f(x2)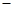 f(x1)(x2
f(x1)(x2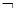 p是
p是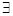 x1,x2
x1,x2