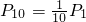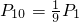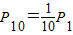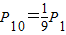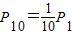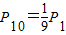Question

盒中有9个黑球、1个白球，它们除颜色不同外，其他方面没有什么差别．现由10个人依次摸出1个球，设第1个人摸出白球的概率为P₁，第10个人摸出白球的概率为P₁₀，则（　　）

• A．P10=

  1

  10

  P1
• B．P10=

  1

  9

  P1
• C．P₁₀=0
• D．P₁₀=P₁

Answer 1

分析：摸球与抽签是一样的，虽然抽签的顺序有先后，但只需不然后人知道先抽人抽出的结果，那么各个抽签者中签的概率是相等的，并不因抽签的顺序不同而影响到其公平性

解答：解：第一个人摸球时，能够摸到白球的概率是P₁=

1

10

如果第一个人没取到 那么第二个人的概率是P2=

9

10

×

1

9

=

1

10

 如果第二个没取到 那么 第三个概率是P3=

9

10

×

8

9

×

1

8

=

1

10

 依此类推 P10=

9

10

×

8

9

×…×

1

2

× 1=

1

10

∴P₁=P₁₀
故选D

点评：本题主要考查了等可能事件的概率求解，解答中容易出现P1=

1

10

，P2=

1

9

，P3=

1

8

的错误，一定要注意事件的基本情况