题目内容
(2009•枣庄一模)已知两条直线m,n,两个平面α,β,给出4个命题:
①若m⊥α,m?β,则β⊥α;
②若α∥β,m∥n,m⊥α,则n⊥β;
③若α∩β=n,且m∥α,m∥β,则m∥n;
④若m∥α,n∥β,m⊥n,则α∥β.
其中正确命题的个数为( )
①若m⊥α,m?β,则β⊥α;
②若α∥β,m∥n,m⊥α,则n⊥β;
③若α∩β=n,且m∥α,m∥β,则m∥n;
④若m∥α,n∥β,m⊥n,则α∥β.
其中正确命题的个数为( )
分析:①利用面面垂直的判定定理判断.②利用线面垂直的判定定理判断.③利用线面平行的性质判断.④利用面面平行的判定定理判断.
解答:解:①根据面面垂直的判定定理可知①正确.
②因为m∥n,m⊥α,所以n⊥α,又α∥β,所以n⊥β,所以②正确.
③根据线面平行的性质可知,③正确.
④因为线面平行和线线垂直不能确定直线的位置关系,所以无法证明α∥β,所以④错误.
故选C.
②因为m∥n,m⊥α,所以n⊥α,又α∥β,所以n⊥β,所以②正确.
③根据线面平行的性质可知,③正确.
④因为线面平行和线线垂直不能确定直线的位置关系,所以无法证明α∥β,所以④错误.
故选C.
点评:本题主要考查空间直线和平面位置关系的判断.要求熟练掌握相应的性质定理和判定定理的应用.

练习册系列答案
 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案
相关题目
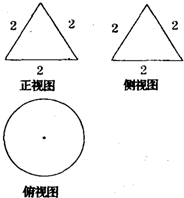 (2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )
(2009•枣庄一模)一个几何体的三视图如图所示,则该几何体外接球的表面积为( )