题目内容
6.设函数f(x)=(x+a)lnx,g(x)=$\frac{{x}^{2}}{{e}^{x}}$.已知曲线y=f(x) 在点(1,f(1))处的切线与直线x+2y-1=0垂直.(Ⅰ)求a的值;
(Ⅱ)设函数m(x)=min{f(x),g(x)}(min{p,q}表示,p,q中的较小值),求函数m(x)的最大值.
分析 (Ⅰ)由两直线垂直的条件:斜率之积为-1,求出函数的导数,可得切线的斜率,解方程可得a=1;
(Ⅱ)运用分段函数的形式写出m(x)的解析式,分别讨论各段的单调性和最值,即可得到所求最大值.
解答 解:(I)由题意知,切线与直线x+2y-1=0垂直,
则曲线f(x)=(x+a)lnx在点(1,f(1))处的切线斜率为2,
所以f′(1)=2,
又f′(x)=lnx+$\frac{a}{x}$+1,即有a+1=2,
所以a=1;
(II)设h(x)-f(x)=(x+1)lnx-$\frac{{x}^{2}}{{e}^{x}}$,
当x∈(0,1]时,h(x)<0.
又h(2)=3ln2-$\frac{4}{{e}^{2}}$=ln8-$\frac{4}{{e}^{2}}$>1-1=0,
所以存在x0∈(1,2),使h(x0)=0.
因为h′(x)=lnx+$\frac{1}{x}$+1+$\frac{x(x-2)}{{e}^{x}}$,
所以当x∈(1,2)时,h′(x)>1-$\frac{1}{e}$>0,
当x∈(2,+∞)时,h′(x)>0,
所以当x>1时,h(x)单调递增.
所以k=1时,方程f(x)=g(x)在(k,k+1)内存在唯一的根x0.
当x∈(0,x0)时,f(x)<g(x),x∈(x0,+∞)时,f(x)>g(x),
所以m(x)=$\left\{\begin{array}{l}{(x+1)lnx,x∈(0,{x}_{0})}\\{\frac{{x}^{2}}{{e}^{2}},x∈({x}_{0},+∞)}\end{array}\right.$.
当x∈(0,x0)时,若x∈(0,1],m(x)≤0,
若x∈(1,x0),由m′(x)=lnx+$\frac{1}{x}$+1>0,可知0<m(x)≤m(x0),故m(x))≤m(x0),
当x∈(x0,+∞)时,由m′(x)=$\frac{x(2-x)}{{e}^{x}}$,
可得x∈(x0,2)时,m′(x)>0,m(x)单调递增;
x∈(2,+∞)时,m′(x)<0,m(x)单调递减;
可知m(x)≤m(2)=$\frac{4}{{e}^{2}}$,且m(x0)<m(2).
综上可得函数m(x)的最大值为$\frac{4}{{e}^{2}}$.
点评 本题考查导数的运用:求切线的斜率和单调区间,考查函数的最值的求法,注意运用单调性,考查运算求解能力,属于中档题.

 阅读快车系列答案
阅读快车系列答案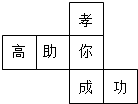 水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )
水平放置的正方体的六个面分别用“前面,后面,上面,下面,左面,右面”表示,如图是正方体的表面展开图,若图中“成”表示正方体的前面,“功”表示正方体的右面,“你”表示正方体的下面,则“孝”“高”“助”分别表示正方体的( )| A. | 左面,后面,上面 | B. | 后面,上面,左面 | C. | 上面,左面,后面 | D. | 后面,左面,上面 |
| A. | [0,$\frac{5}{3}$ ) | B. | [0,$\frac{5}{3}$] | C. | [1,$\frac{5}{3}$ ) | D. | [1,$\frac{5}{3}$] |
| A. | 2 | B. | 3 | C. | 4 | D. | 6 |
| A. | 1 | B. | 2 | C. | 3 | D. | 1或3 |
| A. | -1 | B. | -$\frac{4\sqrt{3}}{9}$ | C. | -2 | D. | -$\frac{2\sqrt{3}}{9}$ |