题目内容
函数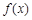 同时满足:①对任意
同时满足:①对任意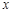 有
有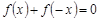 ;②对任意
;②对任意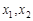 ,当
,当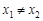 时,有
时,有
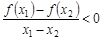 ,则称函数
,则称函数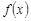 为“理想函数”.给出四个函数:①
为“理想函数”.给出四个函数:①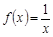 ;②
;②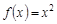 ③
③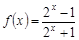 ;④
;④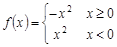 。能被称为“理想函数”的是 .
。能被称为“理想函数”的是 .
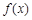 同时满足:①对任意
同时满足:①对任意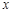 有
有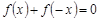 ;②对任意
;②对任意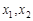 ,当
,当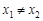 时,有
时,有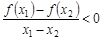 ,则称函数
,则称函数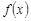 为“理想函数”.给出四个函数:①
为“理想函数”.给出四个函数:①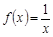 ;②
;②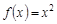 ③
③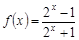 ;④
;④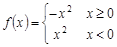 。能被称为“理想函数”的是 .
。能被称为“理想函数”的是 .④
试题分析:首先根据条件可知,①对任意
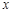 有
有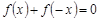 ;②对任意
;②对任意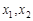 ,当
,当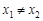 时,有
时,有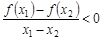 ,则称函数
,则称函数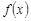 为“理想函数”即说明函数是奇函数,同时在定义域内是减函数,满足题意,由于①
为“理想函数”即说明函数是奇函数,同时在定义域内是减函数,满足题意,由于①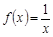 不满足第二个条件,错误;②
不满足第二个条件,错误;②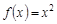 ,不是奇函数,错误。对于③
,不是奇函数,错误。对于③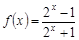 ;不是减函数错误,对于④
;不是减函数错误,对于④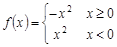 结合分段函数图像可知成立,故答案④
结合分段函数图像可知成立,故答案④点评:主要是考查了函数单调性和奇偶性的综合运用,属于中档题。

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案 寒假创新型自主学习第三学期寒假衔接系列答案
寒假创新型自主学习第三学期寒假衔接系列答案
相关题目
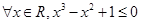 ”的否定为_____________
”的否定为_____________ :Ax+By+C=0(A
:Ax+By+C=0(A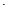 B
B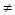 0)垂直的直线方程为: B(x-x0)-A(y-y0)=0;
0)垂直的直线方程为: B(x-x0)-A(y-y0)=0; 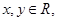 则
则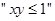 是
是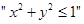 成立的
成立的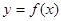 在一点的导数值为
在一点的导数值为 是函数
是函数 ,都有
,都有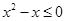 ”的否定是( )
”的否定是( )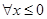 ,都有
,都有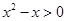
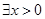 ,使得
,使得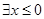 ,使得
,使得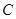 的极坐标方程为
的极坐标方程为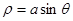 ,则“
,则“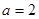 ”是“圆
”是“圆
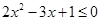 ,命题
,命题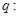
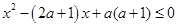 .若
.若 是
是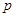 的必要不充分条件,则实数
的必要不充分条件,则实数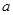 的取值范围是________.
的取值范围是________.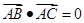 ”是“△ABC为直角三角形”的( ).
”是“△ABC为直角三角形”的( ).