题目内容
(本题12分)一个质地均匀的正四面体的四个面上分别标示着数字1、2、3、4,一个质地均匀的骰子(正方体)的六个面上分别标示数字1、2、3、4、5、6,先后抛掷一次正四面体和骰子。
⑴列举出全部基本事件;
⑵求被压在底部的两个数字之和小于5的概率;
⑶求正四面体上被压住的数字不小于骰子上被压住的数字的概率。
⑴列举出全部基本事件;
⑵求被压在底部的两个数字之和小于5的概率;
⑶求正四面体上被压住的数字不小于骰子上被压住的数字的概率。
⑴ 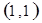
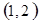
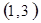
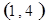
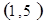
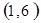
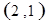
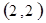
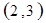
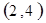
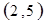
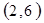
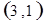
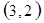
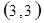
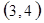
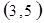
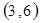
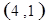
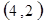
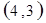
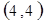
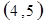
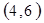
每个基本事件出现的可能性相同.
⑵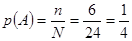 .
.
⑶ .
.
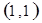
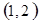
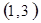
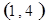
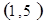
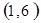
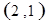
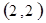
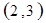
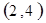
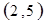
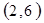
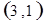
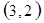
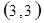
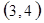
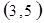
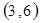
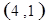
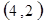
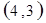
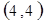
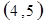
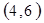
每个基本事件出现的可能性相同.
⑵
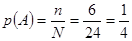 .
. ⑶
 .
. 试题分析:⑴ 用数对
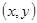 标示正四面体上和骰子上被压住的两个数字,列举所有基本事件如下:
标示正四面体上和骰子上被压住的两个数字,列举所有基本事件如下: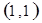
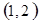
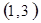
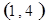
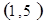
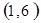
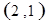
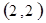
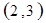
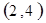
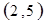
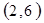
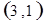
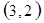
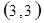
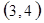
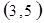
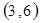
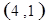
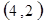
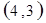
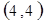
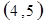
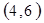
每个基本事件出现的可能性相同. …………………………4分
⑵ 由⑴知基本事件总数
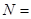 24.
24.设“被压在底部的两个数字之和小于5”为事件
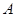 ,则
,则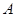 包括
包括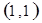 、
、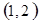 、
、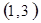 、
、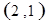 、
、 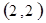 、
、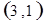 等6个基本事件,事件
等6个基本事件,事件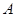 发生的概率
发生的概率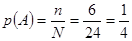 . ………8分
. ………8分⑶ 设“正四面体上被压住的数字不小于骰子上被压住的数字”为事件
 ,则
,则 包括
包括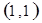 、
、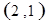 、
、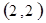 、
、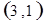 、
、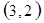 、
、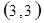 、
、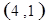 、
、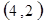 、
、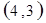 、
、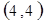 等10个基本事件,事件
等10个基本事件,事件 发生的概率
发生的概率 . ……………………………………12分
. ……………………………………12分点评:基础题,古典概型概率的计算,公式明确,关键是计算基本事件数要准确,可借助于“树图法”“坐标法”。

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目
 个;
个; 个;
个; 个;
个; 个;
个; 个;
个; 个。则样本在区间
个。则样本在区间 上的频率为
上的频率为
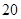 ~
~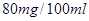 (不含80)之间,属于酒后驾车;在
(不含80)之间,属于酒后驾车;在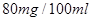 (含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:
(含80)以上时,属于醉酒驾车.某市公安局交通管理部门在某路段的一次拦查行动中,依法检查了300辆机动车,查处酒后驾车和醉酒驾车的驾驶员共20人,检测结果如下表:

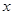
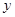 的值为
的值为 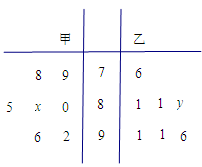
 男 女
男 女 15 7 7 8 9 9 9
15 7 7 8 9 9 9