题目内容
已知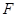 为抛物线
为抛物线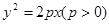 的焦点,抛物线上点
的焦点,抛物线上点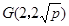 满足
满足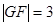

(Ⅰ)求抛物线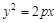 的方程;
的方程;
(Ⅱ) 点的坐标为(
点的坐标为( ,
, ),过点F作斜率为
),过点F作斜率为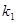 的直线与抛物线交于
的直线与抛物线交于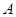 、
、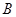 两点,
两点,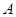 、
、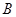 两点的横坐标均不为
两点的横坐标均不为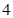 ,连结
,连结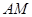 、
、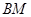 并延长交抛物线于
并延长交抛物线于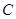 、
、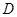 两点,设直线
两点,设直线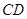 的斜率为
的斜率为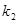 ,问
,问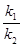 是否为定值,若是求出该定值,若不是说明理由.
是否为定值,若是求出该定值,若不是说明理由.
(Ⅰ)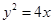 ,(Ⅱ)
,(Ⅱ)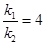 .
.
解析试题分析:(Ⅰ)利用抛物线的定义得到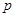 ,再得到方程;(Ⅱ)利用点的坐标表示直线的斜率,设直线的方程,通过联立方程,利用韦达定理计算
,再得到方程;(Ⅱ)利用点的坐标表示直线的斜率,设直线的方程,通过联立方程,利用韦达定理计算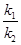 的值.
的值.
试题解析:(Ⅰ)由题根据抛物线定义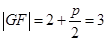 ,
,
所以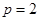 ,所以
,所以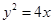 为所求. 2分
为所求. 2分
(Ⅱ)设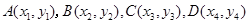
则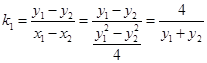 ,同理
,同理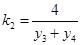 4分
4分
设AC所在直线方程为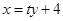 ,
,
联立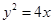 得
得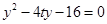 所以
所以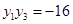 , 6分
, 6分
同理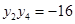 (8分)
(8分)
所以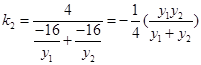 9分
9分
设AB所在直线方程为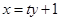 联立
联立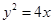
得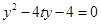 ,
,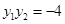 10分
10分
所以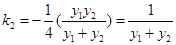
所以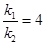 12分
12分
考点:抛物线标准方程,直线与抛物线位置关系的应用.

练习册系列答案
相关题目
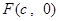 是椭圆
是椭圆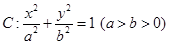 的右焦点,圆
的右焦点,圆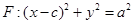 与
与 轴交于
轴交于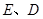 两点,
两点,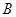 是椭圆
是椭圆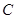 与圆
与圆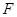 的一个交点,且
的一个交点,且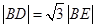
 与
与 ,且
,且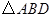 的面积为
的面积为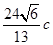 ,求椭圆
,求椭圆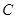 的中心在坐标原点,右准线为
的中心在坐标原点,右准线为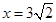 ,离心率为
,离心率为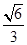 .若直线
.若直线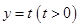 与椭圆
与椭圆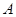 、
、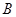 ,以线段
,以线段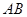 为直径作圆
为直径作圆 .
.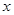 轴相切,求圆
轴相切,求圆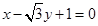 截得的线段长.
截得的线段长.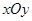 中,已知曲线
中,已知曲线 上任意一点到点
上任意一点到点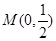 的距离与到直线
的距离与到直线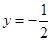 的距离相等.
的距离相等.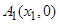 ,
,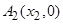 是
是 轴上的两点
轴上的两点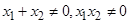 ,过点
,过点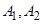 分别作
分别作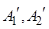 ,直线
,直线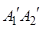 与x轴交于点
与x轴交于点 ,这样就称
,这样就称 确定了
确定了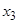 .同样,可由
.同样,可由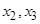 确定了
确定了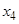 .现已知
.现已知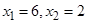 ,求
,求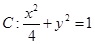 的上、下顶点分别为
的上、下顶点分别为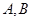 ,点
,点 在椭圆上,且异于点
在椭圆上,且异于点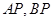 与直线
与直线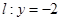 分别交于点
分别交于点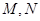 ,
,
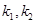 ,求证:
,求证: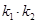 为定值;
为定值;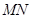 的长的最小值;
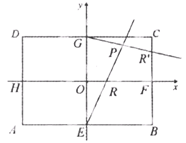
的长的最小值;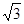 ,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且
,|AD|=2,E、F、G、H分别为矩形四条边的中点,以HF、GE所在直线分别为x,y轴建立直角坐标系(如图所示).若R、R′分别在线段0F、CF上,且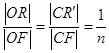 .
.
 :
: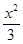 +
+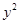 =1上;
=1上;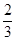 ,求证:直线MN过定点.
,求证:直线MN过定点.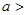
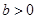 ,曲线
,曲线 上任意一点
上任意一点 分别与点
分别与点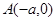 、
、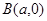 连线的斜率的乘积为
连线的斜率的乘积为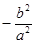 .
.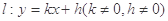 与
与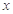 轴、
轴、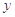 轴分别交于
轴分别交于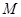 、
、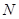 两点,若曲线
两点,若曲线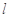 没有公共点,求证:
没有公共点,求证: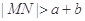 .
.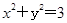 的半径等于椭圆E:
的半径等于椭圆E: (a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x-
(a>b>0)的短半轴长,椭圆E的右焦点F在圆C内,且到直线l:y=x- 的距离为
的距离为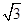 -
-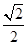 ,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).
,点M是直线l与圆C的公共点,设直线l交椭圆E于不同的两点A(x1,y1),B(x2,y2).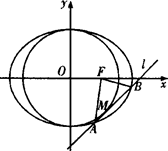
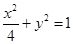 上的三个点,O是坐标原点.
上的三个点,O是坐标原点.