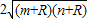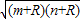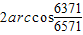题目内容
我国发射的“神舟5号”宇宙飞船的运行轨道是以地球的中心F2为一个焦点的椭圆,近地点A距地面为m千米,远地点B距地面为n千米,地球半径为R千米,则飞船运行轨道的短轴长为( )
分析:因为“神舟5号”宇宙飞船的运行轨道是以地球的中心F2为一个焦点的椭圆,所以近地点距地心为a-c,远地点距地心为a+c.就可求出a,c的值,再根据椭圆中b2=a2-c2求出b,就可得到短轴长.
解答:解:∵“神舟5号”宇宙飞船的运行轨道是以地球的中心F2为一个焦点的椭圆,
设长半轴长为a,短半轴长为b,半焦距为c,
则近地点A距地心为a-c,远地点B距地心为a+c.
∴a-c=m+R,a+c=n+R,
∴a=
+R,c=
.
又∵b2=a2-c2=(
+R)2-(
)2=mn+(m+n)R+R2=(m+R)(n+R)
∴b=
∴短轴长为2b=2
故选A
设长半轴长为a,短半轴长为b,半焦距为c,
则近地点A距地心为a-c,远地点B距地心为a+c.
∴a-c=m+R,a+c=n+R,
∴a=
| m+n |
| 2 |
| n-m |
| 2 |
又∵b2=a2-c2=(
| m+n |
| 2 |
| n-m |
| 2 |
∴b=
| (m+R)(n+R) |
∴短轴长为2b=2
| (m+R)(n+R) |
故选A
点评:本题在实际问题中考查椭圆中a,b,c之间的关系,易错点是没有考虑地球的半径.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
 我国发射的神舟5号飞船开始运行的轨道是以地球的中心F为一个的椭圆,测得近地点A距地面200公里,远地点B距地面350公里,地球的半径为6371公里,则从椭圆轨道上一点看地球的最大视角为( )
我国发射的神舟5号飞船开始运行的轨道是以地球的中心F为一个的椭圆,测得近地点A距地面200公里,远地点B距地面350公里,地球的半径为6371公里,则从椭圆轨道上一点看地球的最大视角为( )