题目内容
如图![]() ,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D
,在四棱柱ABCD-A1B1C1D1中,侧面ADD1A1⊥底面ABCD,D1A=D![]() 1D=
1D=![]() ,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD的中点.
,底面ABCD为直角梯形,其中BC∥AD,AB⊥AD,AD=2AB=2BC=2,O为AD的中点.
(1)求证:A1O∥平面AB1C;
(2)求锐二面角A-C1D1-C的余弦值.
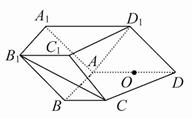
 (1)如图,连接CO,AC,
(1)如图,连接CO,AC,
则四边形ABCO为正方形,
∴OC=AB=A1B1,OC∥AB∥A1B1,
故四边形A1B1C![]() O为平行四边形,
O为平行四边形,
∴A1O∥B1C,
又A1O![]() 平面AB1C,B1C⊂平面AB1C,
平面AB1C,B1C⊂平面AB1C,
∴A1O∥平面AB1C.
(2)∵D1A=D1D,O为AD的中点,∴D1O⊥AD,又侧面ADD1A1⊥底面ABCD,
故D1O⊥底面ABCD,
以O为原点,OC,OD,OD1所在直线分别为x轴,y轴,z轴建立如图所示的空间直角坐标系,
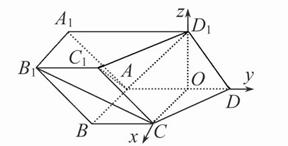
则C(1,0,0),D(0,1,0),D1(0,0,1),A(0,-1,0),
![]() ∴
∴![]() =(1,-1,0),
=(1,-1,0),![]() =(0,-1,1),
=(0,-1,1),![]() =(0,-1,-1),
=(0,-1,-1),![]() =
=![]() =(1,-1,0),
=(1,-1,0),
设m=(x,y,z)为平面CDD1C1的一个法向量,由m⊥![]() ,m⊥
,m⊥![]() ,得
,得![]() ,
,
令z=1,则y=1,x=1,∴m=(1,1,1)
又设n=(x1,y1,z1)为平面AC1D1的一个法向量,由n⊥![]() ,n⊥
,n⊥![]() ,得
,得![]() ,
,
令z1=1,则y1=-1,x1=-1,∴n=(-1,-1,1),
则cos〈m,n〉=![]() =-
=-![]()
![]() ,故所求锐二面角
,故所求锐二面角
A-C1D1-C的余弦值为![]() .
.

练习册系列答案
相关题目
 如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3.
如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2,四棱锥B-AA1C1D的体积为3. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点. 如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
如图,在四棱柱ABC-A1B1C1D1中,AA1⊥底面ABCD,底面ABCD是菱形,∠DAB=60°,AA1=4,AB=2,点E在棱CC1上,点E是棱C1C上一点.
