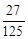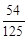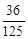题目内容
(本小题满分12分)
已知3名志愿者在10月1号至10月5号期间参加2011年国庆节志愿者活动工作.
(1)若每名志愿者在5天中任选一天参加社区服务工作,且各志愿者的选择互不影响,求3名志原者恰好连续3天参加社区服务工作的概率;
(2)若每名志愿者在这5天中任选两天参加社区服务工作,且各志愿者的选择互不影响,记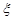 表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量
表示这3名志愿者在10月1号参加志愿者服务工作的人数,求随机变量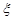 的数学期望.
的数学期望.
【答案】
解:(1)3名志愿者每人任选一天参加社区服务,共有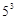 种不同的结果,
种不同的结果,
这些结果出现的可能性都相等.
设“3名志愿者恰好连续3天参加社区服务工作”为事件A,
则该事件共包括 种不同的结果,所以
种不同的结果,所以
答:3名志愿者恰好连续3天参加社区服务工作的概率为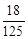 …………6分
…………6分
(II)解法1:随机变量 的可能取值为0,1,2,3
的可能取值为0,1,2,3
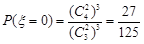 ,
,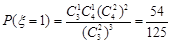
 ,
,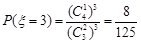 …………8分
…………8分
随机变量ξ的分布列为:
|
|
0 |
1 |
2 |
3 |
|
P |
|
|
|
|
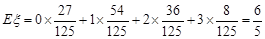
…………12分
解法2:每名志愿者在10月1日参加社区服务的概率均为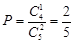
…………8分
则三名志愿者在10月1日参加社区服务的人数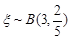
 ,
, …………12分
…………12分
【解析】略

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目