题目内容
14.求值:(1)若x>0,求(2x${\;}^{\frac{1}{4}}$+3${\;}^{\frac{3}{2}}$)(2x${\;}^{\frac{1}{4}}$-3${\;}^{\frac{3}{2}}$)-4x${\;}^{-\frac{1}{2}}$(x-x${\;}^{\frac{1}{2}}$)
(2)lg5(lg8+lg1000)+(lg2${\;}^{\sqrt{3}}$)2+lg$\frac{1}{6}$+lg0.06.
分析 (1)利用指数幂的运算法则即可得出;
(2)利用对数的运算法则即可得出.
解答 解:(1)原式=$4{x}^{\frac{1}{2}}-{3}^{3}$-$4{x}^{\frac{1}{2}}$+4=-23.
(2)原式=lg5(3lg2+3)+3lg22+lg$(\frac{1}{6}×0.06)$
=3lg5lg2+3lg22+3lg5-2
=3lg2(lg5+lg2)+3lg5-2
=3(lg2+lg5)-2
=3-2
=1.
点评 本题考查了指数幂与对数的运算法则,考查了推理能力与计算能力,属于中档题.

练习册系列答案
相关题目
5.已知函数$g(x)=\frac{1}{3}{x^3}+x-m+\frac{m}{x}(m>0)$是[1,∞]上的增函数.当实数m取最大值时,若存在点Q,使得过Q的直线与曲线y=g(x)围成两个封闭图形,且这两个封闭图形的面积总相等,则点Q的坐标为( )
| A. | (0,-3) | B. | (0,3) | C. | (0,-2) | D. | (0,2) |
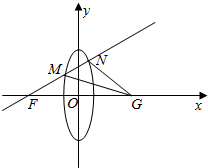 已知,椭圆C:$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0)短轴长是1,离心率e=$\frac{\sqrt{3}}{2}$.
已知,椭圆C:$\frac{{y}^{2}}{{m}^{2}}$+$\frac{{x}^{2}}{{n}^{2}}$=1(m>n>0)短轴长是1,离心率e=$\frac{\sqrt{3}}{2}$.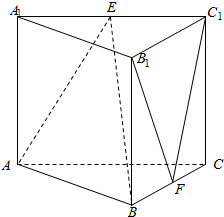 在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F是A1C1、BC的中点.证明:
在直三棱柱ABC-A1B1C1中,AC=4,CB=2,AA1=2,∠ACB=60°,E、F是A1C1、BC的中点.证明: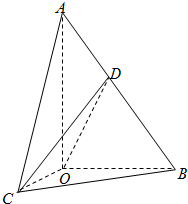 如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上.
如图,在Rt△AOB中,∠OAB=$\frac{π}{6}$,斜边AB=4.Rt△AOC可以通过Rt△AOB以直线AO为轴旋转得到,且二面角B-AO-C是直二面角,动点D在斜边AB上.