题目内容
设n阶方阵
An=
任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则Sn=x1+x2+…+xn,则
=______.
An=
|
任取An中的一个元素,记为x1;划去x1所在的行和列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中的一个元素,记为x2;划去x2所在的行和列,…;将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,则Sn=x1+x2+…+xn,则
| lim |
| n→∞ |
| Sn |
| n3+1 |
不妨取x1=1,x2=2n+3,x3=4n+5,…,xn=2n2-1,
故Sn=1+(2n+3)+(4n+5)+…+(2n2-1)=[1+3+5+…+(2n-1)]+[2n+4n+…+(n-1)2n]=n2+(n-1)×n2=n3,
故
=
=
=1,
故答案为:1.
故Sn=1+(2n+3)+(4n+5)+…+(2n2-1)=[1+3+5+…+(2n-1)]+[2n+4n+…+(n-1)2n]=n2+(n-1)×n2=n3,
故
| lim |
| n→∞ |
| Sn |
| n3+1 |
| lim |
| n→∞ |
| n3 |
| n3+1 |
| lim |
| n→∞ |
| 1 | ||
1+
|
故答案为:1.

练习册系列答案
 时刻准备着暑假作业原子能出版社系列答案
时刻准备着暑假作业原子能出版社系列答案 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案
相关题目
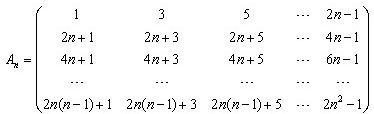
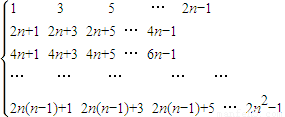
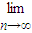
 = .
= .