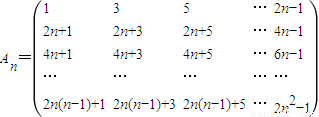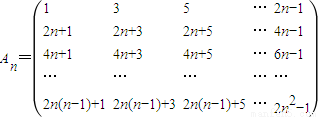题目内容
设n阶方阵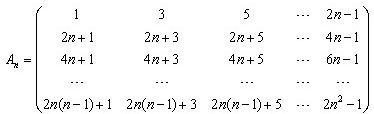
任取An中的一个元素,记为x1;划去x1所在行与列,将剩下的元素按原来的位置关系组成n-1阶方阵An-1,任取An-1中一个元素,记为x2,划去x2所在行与列,…将最后剩下的一个元素记为xn,记Sn=x1+x2+…+xn,若n=3时,则S3=
分析:根据题意可知:令n=3得到三阶矩阵,从中任取一元素得x1,划去x1所在的行和列得到二阶矩阵得到x2,划去x2所在的行和列得到x3,求出之和即可.利用找规律的方法总结出当n=k时Sk的值.
解答:解:当n=3时,A3=
则任取A3中的元素1,划去1所在的行和列得到二阶方阵,则x1=1;
在二阶方阵
中任取一个元素11,划去11所在的行和列则x2=11,
最后剩下15则x3=15,∴S3=x1+x2+x3=1+11+15=27=33;
则当n=k时,根据规律法得到Sk=k3.
故答案为:27;k3.
|
在二阶方阵
|
最后剩下15则x3=15,∴S3=x1+x2+x3=1+11+15=27=33;
则当n=k时,根据规律法得到Sk=k3.
故答案为:27;k3.
点评:本题考查对高阶矩阵中元素的准确认识,以及会用归纳总结得出一般结论的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目