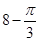题目内容
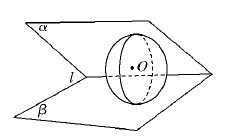
(理)球O与锐二面角α-l-β的两半平面相切,两切点间的距离为,O点到交线l的距离为2,则球O的表面积为( )

| A. | B.4π | C.12π | D.36π |
B
试题分析:设球O与平面α,β分别切于点P,Q,过点O作OR
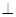 l于低能R,连接PR,QR,PQ,设PQ与OR相交于点S,其抽象图如下图所示,则有PO
l于低能R,连接PR,QR,PQ,设PQ与OR相交于点S,其抽象图如下图所示,则有PO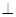 PR,OQ
PR,OQ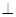 QR,故P,O,Q,R四点共圆,此圆的直径为2,由正弦定理得
QR,故P,O,Q,R四点共圆,此圆的直径为2,由正弦定理得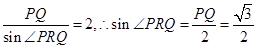 ,又二面角α-l-β为锐二面角,所以
,又二面角α-l-β为锐二面角,所以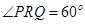
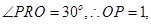 即球的半径为1,球O的表面积为S=
即球的半径为1,球O的表面积为S=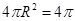 ,故选B.
,故选B.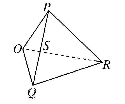
点评:解决该试题的关键是从空间几何体中抽象出要解决的四面体,然后通过解三角形和二面角得到结论,属于中等难度试题,考查了空间的想象能力。

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
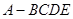 的侧面
的侧面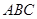 是等边三角形,
是等边三角形,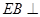 平面
平面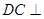 平面
平面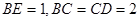 ,
,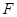 是棱
是棱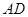 的中点.
的中点.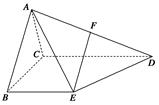
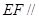 平面
平面 )可知这个几何体的表面积为( )
)可知这个几何体的表面积为( )

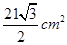


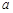 的正方体有一内切球,该球的表面积为
的正方体有一内切球,该球的表面积为
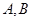 到平面
到平面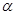 的距离分别为
的距离分别为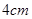 和
和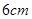 ,当线段AB与平面
,当线段AB与平面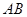 的中点
的中点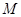 到
到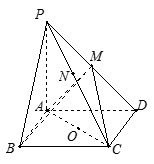
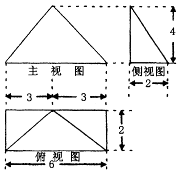
 的正方形,两条虚线互相垂直,则该几何体的体积是( )
的正方形,两条虚线互相垂直,则该几何体的体积是( )