题目内容
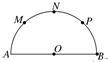
如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点(1)从A、B、M、N、P这5个点中任取3个点,求这3个点组成直角三角形的概率;
(2)在半圆内任取一点S,求三角形SAB的面积大于8
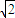 的概率.
的概率.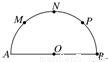
【答案】分析:(1)这是一个古典概型问题,我们可以列出从A、B、M、N、P这5个点中任取3个点,可能组成的所有三角形的个数,然后列出其中是直角三角形的个数,代入古典概型公式即可求出答案.
(2)这是一个几何概型问题,我们可以求出所有事件对应平面区域的面积,再求出满足条件平面区域面积,代入几何概型公式即可求出答案.
解答:解:(1)从A、B、M、N、P这5个点中任取3个点,一共可以组成10个三角形:ABM、ABN、ABP、AMN、AMP、ANP、BMN、BMP、BNP、MNP,其中是直角三角形的只有ABM、ABN、ABP3个,
所以这3个点组成直角三角形的概率P=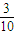 .
.
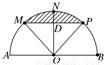 (2)连接MP,取线段MP的中点D,则OD⊥MP,
(2)连接MP,取线段MP的中点D,则OD⊥MP,
易求得OD=2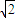 ,
,
当S点在线段MP上时,S△ABS= ×2
×2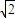 ×8=8
×8=8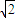 ,
,
所以只有当S点落在阴影部分时,三角形SAB面积才能大于8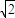 ,而
,而
S阴影=S扇形OMP-S△OMP= ×
×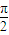 ×42-
×42- ×42=4π-8,
×42=4π-8,
所以由几何概型公式得三角形SAB的面积大于8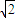 的概率P=
的概率P=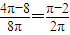 .
.
点评:本题考查的是几何概型和古典概型,掌握几何概型和古典概型的计算步骤和计算公式是解答本题的关键.
(2)这是一个几何概型问题,我们可以求出所有事件对应平面区域的面积,再求出满足条件平面区域面积,代入几何概型公式即可求出答案.
解答:解:(1)从A、B、M、N、P这5个点中任取3个点,一共可以组成10个三角形:ABM、ABN、ABP、AMN、AMP、ANP、BMN、BMP、BNP、MNP,其中是直角三角形的只有ABM、ABN、ABP3个,
所以这3个点组成直角三角形的概率P=
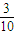 .
. (2)连接MP,取线段MP的中点D,则OD⊥MP,
(2)连接MP,取线段MP的中点D,则OD⊥MP,易求得OD=2
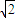 ,
,当S点在线段MP上时,S△ABS=
 ×2
×2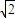 ×8=8
×8=8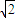 ,
,所以只有当S点落在阴影部分时,三角形SAB面积才能大于8
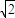 ,而
,而S阴影=S扇形OMP-S△OMP=
 ×
×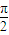 ×42-
×42- ×42=4π-8,
×42=4π-8,所以由几何概型公式得三角形SAB的面积大于8
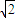 的概率P=
的概率P=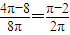 .
.点评:本题考查的是几何概型和古典概型,掌握几何概型和古典概型的计算步骤和计算公式是解答本题的关键.

练习册系列答案
相关题目
 如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点
如图,已知AB是半圆O的直径,AB=8,M、N、P是将半圆圆周四等分的三个分点 (2013•许昌三模)如图,已知C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.
(2013•许昌三模)如图,已知C是以AB为直径的半圆O上一点,CH⊥AB于点H,直线AC与过B点的切线相交于点D,E为CH中点,连接AE并延长交BD于点F,直线CF交直线AB于点G.